
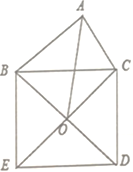
【题目】如图,在△ABC中,AB=4,AC=3,以BC为边在三角形外作正方形BCDE,对角线BD、CE交于点O,则线段AO的最大值为_____.
【答案】![]()
【解析】
过O作OF⊥AO且使OF=AO,连接AF、CF,可知△AOF是等腰直角三角形,进而可得AF=![]() AO,根据正方形的性质可得OB=OC,∠BOC=90°,由锐角互余的关系可得∠AOB=∠COF,进而可得△AOB≌△COF,即可证明AB=CF,当点A、C、F三点不共线时,根据三角形的三边关系可得AC+CF>AF,当点A、C、F三点共线时可得AC+CF=AC+AB=AF=7,即可得AF的最大值,由AF=
AO,根据正方形的性质可得OB=OC,∠BOC=90°,由锐角互余的关系可得∠AOB=∠COF,进而可得△AOB≌△COF,即可证明AB=CF,当点A、C、F三点不共线时,根据三角形的三边关系可得AC+CF>AF,当点A、C、F三点共线时可得AC+CF=AC+AB=AF=7,即可得AF的最大值,由AF=![]() AO即可得答案.
AO即可得答案.
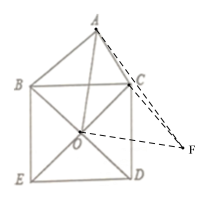
如图,过O作OF⊥AO且使OF=AO,连接AF、CF,
∴∠AOF=90°,△AOF是等腰直角三角形,
∴AF=![]() AO,
AO,
∵四边形BCDE是正方形,
∴OB=OC,∠BOC=90°,
∵∠BOC=∠AOF=90°,
∴∠AOB+∠AOC=∠COF+∠AOC,
∴∠AOB=∠COF,
又∵OB=OC,AO=OF,
∴△AOB≌△COF,
∴CF=AB=4,
当点A、C、F三点不共线时,AC+CF>AF,
当点A、C、F三点共线时,AC+CF=AC+AB=AF=7,
∴AF≤AC+CF=7,
∴AF的最大值是7,
∴AF=![]() AO=7,
AO=7,
∴AO=![]() .
.
故答案为:![]()


 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案科目:初中数学 来源: 题型:
【题目】某商场经营某种品牌的玩具,进价是![]() 元,根据市场调查:在一段时间内,销售单价是
元,根据市场调查:在一段时间内,销售单价是![]() 元时,销售量是
元时,销售量是![]() 件,而销售单价每涨
件,而销售单价每涨![]() 元,就会少售出
元,就会少售出![]() 件玩具.
件玩具.
(1)不妨设该种品牌玩具的销售单价为![]() 元
元![]() ,请你分别用
,请你分别用![]() 的代数式来表示销售量
的代数式来表示销售量![]() 件和销售该品牌玩具获得利润
件和销售该品牌玩具获得利润![]() 元,并把结果填写在表格中:
元,并把结果填写在表格中:
(2)在![]() 问条件下,若商场获得了
问条件下,若商场获得了![]() 元销售利润,求该玩具销售单价
元销售利润,求该玩具销售单价![]() 应定为多少元.
应定为多少元.
(3)在![]() 问条件下,求商场销售该品牌玩具获得的最大利润是多少?此时定价多少元?
问条件下,求商场销售该品牌玩具获得的最大利润是多少?此时定价多少元?
销售单价(元) |
|
销售量 | |
销售玩具获得利润 |
|
查看答案和解析>>
科目:初中数学 来源: 题型:
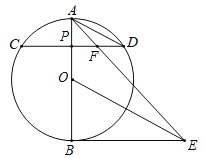
【题目】如图,AB为⊙O直径,P点为半径OA上异于O点和A点的一个点,过P点作与直径AB垂直的弦CD,连接AD,作BE⊥AB,OE∥AD交BE于E点,连接AE、DE、AE交CD于F点.
(1)求证:DE为⊙O切线;
(2)若⊙O的半径为3,sin∠ADP=![]() ,求AD;
,求AD;
(3)请猜想PF与FD的数量关系,并加以证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点C在AB为直径的圆O上,AD与过点C的切线垂直,垂足为点D,AD交圆O于点E.
(1)求证:AC平分∠DAB;
(2)连接BE,若BE=6,sin∠CAD=![]() ,求圆O的半径.
,求圆O的半径.

查看答案和解析>>
科目:初中数学 来源: 题型:
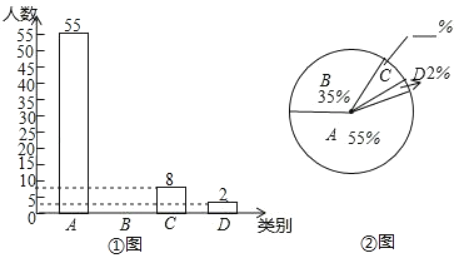
【题目】我省某地区为了了解2017年初中毕业生毕业去向,对部分九年级学生进行了抽样调查,就九年级学生毕业后的四种去向:A.读重点高中;B.读职业高中;C.直接进入社会就业;D.其他(如出国等)进行数据统计,并绘制了两幅不完整的统计图(如①图,如②图)
(1)该地区共调查了_____名九年级学生;
(2)将两幅统计图中不完整的部分补充完整;
(3)若该地区2017年初中毕业生共有4000人,请估计该地区今年初中毕业生中读重点高中的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
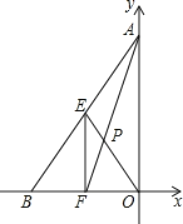
【题目】如图,在平面直角坐标系中,O为坐标原点,点A,B的坐标分别为(0,4),(﹣3,0),E为AB的中点,EF∥AO交OB于点F,AF与EO交于点P,则EP的长为_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com