
请你写出一个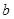 的值,使得函数
的值,使得函数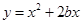 在第一象限内
在第一象限内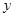 的值随着
的值随着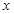 的值增大而增大,则
的值增大而增大,则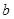 可以是 .
可以是 .
答案不唯一,如0;1;2等
【解析】
试题分析:将函数y=x2+2bx化为y=(x+b)2-b2,可得对称轴为x=-b,当图象在对称轴右侧,y随着x的增大而增大;而在对称轴左侧,y随着x的增大而减小,所以对称轴不能过第一象限,即-b≤0,得b≥0.
因为a=1>0,抛物线开口向上,
又函数y=x2+2bx在第一象限内y的值随着x的值增大而增大,
所以对称轴不能过第一象限,即x=-b≤0,得b≥0.
在此范围内确定b的值.本题答案不唯一,如:0,1,2等.
考点:本题综合考查二次函数的增减性
点评:解答本题的关键是根据函数关系式得到当图象在对称轴右侧,y随着x的增大而增大;而在对称轴左侧,y随着x的增大而减小。


 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
 学校围墙边有一个直角三角形的花圃(如图1所示的Rt△ABC),其中斜边AB借助围墙,两条直角边AC和BC用铁栅栏围成,已知AB=10米,AC=8米.
学校围墙边有一个直角三角形的花圃(如图1所示的Rt△ABC),其中斜边AB借助围墙,两条直角边AC和BC用铁栅栏围成,已知AB=10米,AC=8米.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com