
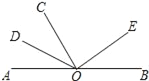
【题目】如图,点O在直线AB上,OD是∠AOC的平分线,射线OE在∠BOC内.
(1)图中有多少个小于180°的角?
(2)若OE平分∠BOC,求∠DOE的度数;
(3)若∠COE=2∠BOE,∠DOE=108°,求∠COE的度数.
【答案】(1)图中有9个小于180°的角;(2)∠DOE=90°;(3)∠COE═72°.
【解析】
(1)根据角的定义,按照一定的规律计数即可;
(2)依据角平分线的定义可知∠COD=![]() ∠AOC,∠COE=
∠AOC,∠COE=![]() ∠BOC,然后逆用乘法的分配律可求得∠DOE=90°;
∠BOC,然后逆用乘法的分配律可求得∠DOE=90°;
(3)设∠BOE=x,然后依据∠DOE=108°列方程求解即可.
(1)图中小于180°的角有∠AOD、∠AOC、∠AOE、∠DOC、∠DOE、∠DOB、∠COE、∠COB、∠EOB共9个;
(2)∵OD平分∠AOC,OE平分∠BOC,
∴![]() ,
,![]() .
.
∵∠AOC+∠BOC=180°,
∴![]() .
.
∴∠DOE=∠COD+∠COE=90°.
(3)设∠BOE=x,
∵∠COE=2∠BOE,∴∠COE=2x,
∴∠AOC=180°﹣3x.
∵OD平分∠AOC,
∴![]() .
.
∵∠COD+∠COE═∠DOE=108°,
∴![]() ,x=36°.
,x=36°.
∴∠COE═72°.


 优加精卷系列答案
优加精卷系列答案科目:初中数学 来源: 题型:
【题目】如图,点A的坐标为(1,2),AB⊥x轴于点B,将△AOB绕点A逆时针旋转90°得到△ACD,双曲线y= ![]() (x>0)恰好经过点C,交AD于点E,则点E的坐标为 .
(x>0)恰好经过点C,交AD于点E,则点E的坐标为 . 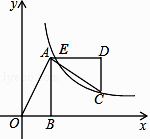
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD的对角线AC和BD交于点O,则下列不能判断四边形ABCD是平行四边形的条件是( )
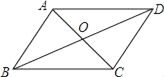
A. OA=OC,AD∥BC B. ∠ABC=∠ADC,AD∥BC
C. AB=DC,AD=BC D. ∠ABD=∠ADB,∠BAO=∠DCO
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,制作一种产品的同时,需要将原材料加热,设该材料温度为y℃,从加热开始计算的时间为x分钟,据了解,该材料在加热过程中温度y与时间x成一次函数关系,已知该材料在加热前的温度为15℃,加热5分钟使材料温度达到60℃时停止加热.停止加热后,材料温度逐渐下降,这时温度y与时间x成反比例函数关系. 
(1)分别求出该材料加热过程中和停止加热后y与x之间的函数表达式,并写出x的取值范围;
(2)根据工艺要求,在材料温度不低于30℃的这段时间内,需要对该材料进行特殊处理,那么对该材料进行特殊处理所用的时间是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,数轴的单位长度为1,如果P,Q表示的数互为相反数,那么图中的4个点中,哪一个点表示的数的平方值最大( )
![]()
A. P B. R C. Q D. T
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解:如图1,在平面内选一定点O,引一条有方向的射线Ox,再选定一个单位长度,那么平面上任一点M的位置可由∠MOx的度数θ与OM的长度m确定,有序数对(θ,m)称为M点的“极坐标”,这样建立的坐标系称为“极坐标系”. 应用:在图2的极坐标系下,如果正六边形的边长为2,有一边OA在射线Ox上,则正六边形的顶点C的极坐标应记为( )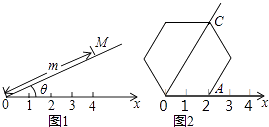
A.(60°,4)
B.(45°,4)
C.(60°,2 ![]() )
)
D.(50°,2 ![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市为解决部分市民冬季集中取暖问题需铺设一条长3000米的管道,为尽量减少施工对交通造成的影响,实施施工时“…”,设实际每天铺设管道x米,则可得方程 ![]() ,根据此情景,题中用“…”表示的缺失的条件应补为( )
,根据此情景,题中用“…”表示的缺失的条件应补为( )
A.每天比原计划多铺设10米,结果延期15天才完成
B.每天比原计划少铺设10米,结果延期15天才完成
C.每天比原计划多铺设10米,结果提前15天才完成
D.每天比原计划少铺设10米,结果提前15天才完成
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知反比例函数 ![]() 的图象与一次函数y2=ax+b的图象交于点A(1,4)和点B(m,﹣2),
的图象与一次函数y2=ax+b的图象交于点A(1,4)和点B(m,﹣2), 
(1)求这两个函数的关系式;
(2)观察图象,写出使得y1>y2成立的自变量x的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com