
已知抛物线L:y=ax2+bx+c(其中a、b、c都不等于0),它的顶点P的坐标是(-![]() ,
,![]() ),与y轴的交点是M(0,c).我们称以M为顶点,对称轴是y轴且过点P的抛物线为抛物线L的伴随抛物线,直线PM为L的伴随直线.
),与y轴的交点是M(0,c).我们称以M为顶点,对称轴是y轴且过点P的抛物线为抛物线L的伴随抛物线,直线PM为L的伴随直线.
(1)请直接写出抛物线y=2x2-4x+1的伴随抛物线和伴随直线的解析式:
伴随抛物线的解析式________,
伴随直线的解析式________;
(2)若一条抛物线的伴随抛物线和伴随直线分别是y=-x2-3和y=-x-3,则这条抛物线的解析式是________;
(3)求抛物线L:y=ax2+bx+c(其中a、b、c都不等于0)的伴随抛物线和伴随直线的解析式;
(4)若抛物线L与x轴交于A(x1,0),B(x2,0)两点,x2>x1>0,它的伴随抛物线与x轴交于C、D两点,且AB=CD,请求出a、b、c应满足的条件.
|
分析:由抛物线 y=2x2-4x+1的顶点为(1,-1),与y轴的交点为(0,1),那么它的伴随抛物线的顶点为(0,1),且过点(1,-1).由于顶点在 y轴上,因此可设伴随抛物线解析式为y=ax2+1,再把(1,-1)代入,可求得a=-2,所以求得伴随抛物线为y=-2x2+1.伴随直线是过 (0,1),(1,-1)两点的直线,设直线解析式为y=px+q,则
所以伴随抛物线为 y=-2x+1.(2)若已知一条抛物线的伴随抛物线与伴随直线分别为y=-x2-3与y=-x-3,而它们在y轴的交点(0,-3)是原抛物线上的点,这两条图像的另一个交点是原抛物线的顶点,为了求这两个图像的交点,可解方程组
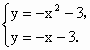 解得 解得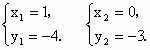
而 (0,-3)就是两个图像在y轴上的交点,则另一点(1,-4)就是原抛物线的顶点.设抛物线的解析式为 y=m(x-1)2-4,把(0,3)代入,m=1,所以y=(x-1)2-4=x2-2x-3.(3)求抛物线y=ax2+bx+c(其中a、b、c都不为0)的伴随抛物线与伴随直线解析式的一般形式,由定义可知,伴随抛物线的顶点是(0,c),设它的解析式为y=mx2+c(m≠0)(对称轴为y轴b=0). ∵抛物线过原抛物线的顶点 P(-∴ ∴伴随抛物线的解析式为 y=-ax2+c.设伴随直线解析式为 y=kx+c.∵ P(-∴伴随直线的解析式为 y=(4)由x2>x1>0,且AB=CD,则可用a、b、c表示出AB、CD的长. ∵抛物线 L与x轴有两个交点,∴Δ1=b2-4ac>0,∴b2>4ac.∵ x2>x1>0,∴x1+x2=-∴ ad<0,ac>0.对于伴随抛物线 y=-ax2+c,有Δ2=02-(-4ac)=4ac>0,由- ax2+c=0,得x=±∴ CD=2又 AB=x2-x1=由 AB=CD,得综上所述 b2>4ac,ab<0,ac>0,b2=8ac.所以 a、b、c应满足的条件为b2=8ac且ab<0(或bc>0). |


 激活思维优加课堂系列答案
激活思维优加课堂系列答案 活力试卷系列答案
活力试卷系列答案科目:初中数学 来源: 题型:044
如图,已知抛物线P:y=ax2+bx+c(a≠0) 与x轴交于A、B两点(点A在x轴的正半轴上),与y轴交于点C,矩形DEFG的一条边DE在线段AB上,顶点F、G分别在线段BC、AC上,抛物线P上部分点的横坐标对应的纵坐标如下:
|
x |
… |
-3 |
-2 |
1 |
2 |
… |
|
y |
… |
- |
-4 |
- |
0 |
… |
(1)
求A、B、C三点的坐标;(2)
若点D的坐标为(m,0),矩形DEFG的面积为S,求S与m的函数关系,并指出m的取值范围;(3)
当矩形DEFG的面积S取最大值时,连接DF并延长至点M,使FM=k·DF,若点M不在抛物线P上,求k的取值范围.
查看答案和解析>>
科目:初中数学 来源:2013年浙江省金华、丽水市高级中等学校招生考试数学 题型:044
如图,已知抛物线![]() 与直线y=2x交于点O(0,0),A(a,12),点B是抛物线上O,A之间的一个动点,过点B分别作x轴、y轴的平行线与直线OA交于点C,E.
与直线y=2x交于点O(0,0),A(a,12),点B是抛物线上O,A之间的一个动点,过点B分别作x轴、y轴的平行线与直线OA交于点C,E.

(1)求抛物线的函数解析式;
(2)若点C为OA的中点,求BC的长;
(3)以BC,BE为边构造矩形BCDE,设点D的坐标为(m,n),求出m,n之间的关系式.
查看答案和解析>>
科目:初中数学 来源:2007中考夺标冲刺模拟题(新课标)(二)、数学 题型:044
如图,已知抛物线![]() 与直线y=x交于A、B两点,与y轴交于点C,OA=OB,BC∥x轴.
与直线y=x交于A、B两点,与y轴交于点C,OA=OB,BC∥x轴.

(1)求抛物线的解析式.
(2)设D、E是线段AB上异于A、B的两个动点(点E在点D的上方),DE=![]() ,过D、E两点分别作y轴的平行线,交抛物线于F、G,若设D点的横坐标为x,四边形DEGF的面积为y,求x与y之间的关系式,写出自变量x的取值范围,并回答x为何值时,y有最大值.
,过D、E两点分别作y轴的平行线,交抛物线于F、G,若设D点的横坐标为x,四边形DEGF的面积为y,求x与y之间的关系式,写出自变量x的取值范围,并回答x为何值时,y有最大值.
查看答案和解析>>
科目:初中数学 来源:湖北省十堰市2006年课改实验区初中毕业生学业考试数学 题型:044
已知抛物线C1:y=-x2+2mx+n(m,n为常数,且m≠0,n>0)的顶点为A,与y轴交于点C;抛物线C2与抛物线C1关于y轴对称,其顶点为B,连接AC,BC,AB.
注:抛物线y=ax2+bx+c(a≠0)的顶点坐标为![]() .
.
(1)请在横线上直接写出抛物线C2的解析式:________;
(2)当m=1时,判定△ABC的形状,并说明理由;
(3)抛物线C1上是否存在点P,使得四边形ABCP为菱形?如果存在,请求出m的值;如果不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源:2007年资阳市初中毕业升学统一考试、数学试卷 题型:059
如图,已知抛物线P:y=ax2+bx+c(a≠0)与x轴交于A、B两点(点A在x轴的正半轴上),与y轴交于点C,矩形DEFG的一条边DE在线段AB上,顶点F、G分别在线段BC、AC上,抛物线P上部分点的横坐标对应的纵坐标如下:


(1)求A、B、C三点的坐标;
(2)若点D的坐标为(m,0),矩形DEFG的面积为S,求S与m的函数关系,并指出m的取值范围;
(3)当矩形DEFG的面积S取最大值时,连接DF并延长至点M,使FM=k·DF,若点M不在抛物线P上,求k的取值范围.
若因为时间不够等方面的原因,经过探索、思考仍无法圆满解答本题,请不要轻易放弃,试试将上述(2)、(3)小题换为下列问题解答(已知条件及第(1)小题与上相同,完全正确解答只能得到5分):
(2)若点D的坐标为(1,0),求矩形DEFG的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com