练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    计算： _________________．

    x3+y3; 【解析】原式=?x²y+xy²+x²y?xy²+=?x²y+xy²+x²y?xy²+=
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：山东省德州地区2017-2018学年度九年级第一学期期末检测数学试卷 题型：填空题

    若一元二次方程有实数根，则m的取值范围是_______ 。

    【解析】试题解析：关于的一元二次方程 有实数根， 解得： 故答案为：

    查看答案和解析>>

    科目：初中数学 来源：2018人教版九年级数学下册练习：第二十八章 达标检测卷 题型：解答题

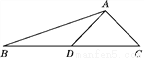
    如图，AD是△ABC的中线，tan B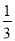＝，cos C＝，AC＝.求：

    （1）BC的长；

    （2）sin ∠ADC的值．

    （1）BC＝4；（2）sin ∠ADC＝. 【解析】（1）如图，作AE⊥BC， ∴CE=AC•cosC=1，∴AE=CE=1， ， ∴BE=3AE=3，∴BC=4； （2）∵AD是△ABC的中线，∴DE=1， ∴∠ADC=45°，∴．

    查看答案和解析>>

    科目：初中数学 来源：河南省周口市西华县2017-2018学年八年级上学期期末考试数学试卷 题型：解答题

    如图（1），在四边形ABCD中，已知∠ABC∠ADC180°，ABAD，ABAD，点E在CD的延长线上，∠1∠2．

    （1）求证：∠3∠E；

    （2）求证：CA平分∠BCD；

    （3）如图（2），设AF是△ABC的边BC上的高，求证：CE2AF．

    （1）证明见解析；（2）证明见解析；（3）证明见解析. 【解析】分析：（1）根据三角形的判定定理ASA即可证得．（2）通过三角形全等求得AC=AE，∠BCA=∠E，进而根据等边对等角求得∠ACD=∠E，从而求得∠BCA=∠E=∠ACD即可证得．（3）过点A作AM⊥CE，垂足为M，根据角的平分线的性质求得AF=AM，然后证得△CAE和△ACM是等腰直角三角形，进而证得EC=2AF． 本题...

    查看答案和解析>>

    科目：初中数学 来源：河南省周口市西华县2017-2018学年八年级上学期期末考试数学试卷 题型：解答题

    分解因式：① -a4+16；②6xy2-9x2y-y3

    （1）（2-a）(2+a)(4+a2)；（2）-y2(y-3x)2. 【解析】分析：（1）利用平方差公式分解即可；（2）先提公因式，再利用完全平方公式分解即可. 本题解析： (1) （2）

    查看答案和解析>>

    科目：初中数学 来源：河南省周口市西华县2017-2018学年八年级上学期期末考试数学试卷 题型：单选题

    点A（a + 1，a）关于x轴对称的点在第一象限，则a的取值范围是（ ）

    A. -1< a < 0 B. 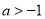C. D.

    A 【解析】∵点A(a+1,a)关于x轴的对称点在第一象限， ∴点A(a+1,a)在第四象限， ∴， 解得：-1

    查看答案和解析>>

    科目：初中数学 来源：2017-2018学年七年级数学北师大版上册 第1章 丰富的图形世界 单元测试卷 题型：解答题

    如图所示，长方形ABCD的长AB为10 cm，宽AD为6 cm，把长方形ABCD绕AB边所在的直线旋转一周，然后用平面沿AB方向去截所得的几何体，求截面的最大面积．

    120cm2 【解析】试题分析：长方形ABCD绕直线AB旋转一周得到一个圆柱体，沿线段AB的方向截所得的几何体其中轴截面最大． 试题解析：【解析】 由题可得，把长方形ABCD绕AB边所在的直线旋转一周，得到的几何体为圆柱，圆柱的底面半径为6cm，高为10cm，∴截面的最大面积为6×2×10=120（cm2）．

    查看答案和解析>>

    科目：初中数学 来源：2017-2018学年七年级数学北师大版上册 第1章 丰富的图形世界 单元测试卷 题型：单选题

    下列几何体没有曲面的是( )

    A. 圆锥 B. 圆柱 C. 球 D. 棱柱

    D 【解析】解：A．圆锥由一个平面和一个曲面组成，不符合题意； B．圆柱由2个平面和一个曲面组成，不符合题意； C．球由一个曲面组成，不符合题意； D．棱柱是由多个平面组成，符合题意． 故选D．

    查看答案和解析>>

    科目：初中数学 来源：广东省汕头市澄海区2017-2018学年八年级上学期期末质量检测数学试卷 题型：解答题

    已知△ABC的三边长， ， 满足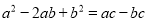，试判断△ABC的形状，并说明理由．

    △ABC为等腰三角形 【解析】试题分析：把等式整理后，因式分解即可得到结论． 试题解析：【解析】 △ABC为等腰三角形．理由如下： ∵， ∴， ∴， ∴． ∵、、是△ABC的三边长， ∴， ∴， ∴， ∴△ABC为等腰三角形．

    查看答案和解析>>

    同步练习册答案