
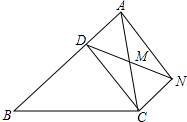
 已知:如图,D是△ABC的边AB上一点,CN∥AB,DN交AC于点M,若MA=MC,∠BAN=90°,求证:四边形ADCN是矩形.
已知:如图,D是△ABC的边AB上一点,CN∥AB,DN交AC于点M,若MA=MC,∠BAN=90°,求证:四边形ADCN是矩形. 分析 通过证明△AMD≌△CMN得到对应边AD=CN;结合已知条件“CN∥AB”判定四边形ADCN是平行四边形;再根据“有一内角为直角的平行四边形是矩形”证得结论.
解答 证明:∵CN∥AB,
∴∠DAC=∠NCA,
在△AMD和△CMN中,
∵$\left\{\begin{array}{l}{∠DAC=∠NCA}\\{MA=MC}\\{∠AMD=∠CMN}\end{array}\right.$,
∴△AMD≌△CMN(ASA),
∴AD=CN.
又∵AD∥CN,
∴四边形ADCN是平行四边形.
又∵∠BAN=90度,
∴四边形ADCN是矩形.
点评 本题考查了矩形的判定.题设中出现一个直角或垂直时,常采用“有一个角是直角的平行四边形是矩形”来判定矩形.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
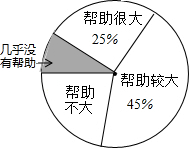 为了解“数学思想作文对学习帮助有多大?”研究员随机抽取了一定数量的高校大一学生进行了问卷调查,并将调查得到的数据用下面的扇形图和如表来表示(图、表都没制作完成).
为了解“数学思想作文对学习帮助有多大?”研究员随机抽取了一定数量的高校大一学生进行了问卷调查,并将调查得到的数据用下面的扇形图和如表来表示(图、表都没制作完成).| 选项 | 帮助很大 | 帮助较大 | 帮助不大 | 几乎没有帮助 |
| 人数 | a | 540 | 270 | b |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
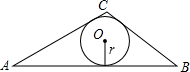 已知任意三角形的三边长,如何求三角形面积?
已知任意三角形的三边长,如何求三角形面积?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
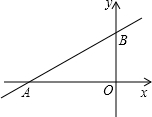 如图,一次函数y=kx+b图象经过点A(-4,0)和点B(0,2),
如图,一次函数y=kx+b图象经过点A(-4,0)和点B(0,2),查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 不变 | B. | 扩大2倍 | C. | 缩小2倍 | D. | 扩大4倍 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 在平面直角坐标系中,平行四边形OABC的边OC落在x轴的正半轴上,且点C(4,0),B(6,2),直线y=2x+1以每秒1个单位的速度向下平移,经过6秒该直线可将平行四边形OABC的面积平分.
在平面直角坐标系中,平行四边形OABC的边OC落在x轴的正半轴上,且点C(4,0),B(6,2),直线y=2x+1以每秒1个单位的速度向下平移,经过6秒该直线可将平行四边形OABC的面积平分.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com