
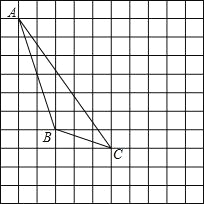
【题目】如图,每个小正方形的边长为 1 个单位,每个小方格的顶点叫格点.
(1)画出△ABC 的 AB 边上的中线 CD;
(2)画出△ABC 向右平移 4 个单位后得到的△A1B1C1;
(3)图中 AC 与 A1C1 的关系是: ;
(4)图中△ABC 的面积是 ;
(5)能使△BCE 面积为 3 的格点 E 有 个.
【答案】(1)见解析;(2)见解析;(3)AC 与 A1C1 平行且相等;(4)8;(5)8
【解析】(1)根据网格结构确定出AB的中点D,然后连接CD即可;
(2)根据网格结构找出点A、B、C向右平移4个单位后的对应点A1、B1、C1的位置,然后顺次连接即可;
(3)根据平移的性质解答;
(4)利用△ABC所在的矩形的面积减去四周三个直角三角形的面积和一个小长方形的面积,列式计算即可得解;
(5)首先分别在BC的两侧找到一个使其面积是3个平方单位的点E,再分别过这两点作BC的平行线,找到所有的格点即可.
(1)中线CD如图所示;
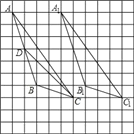
(2)△A1B1C1如图所示;
(3)AC与 A1C1平行且相等;
(4)△ABC的面积=5×7﹣![]() ×6×2﹣
×6×2﹣![]() ×3×1﹣
×3×1﹣![]() ×5×7﹣2×1=35﹣6﹣1.5﹣17.5﹣2=35﹣27=8;
×5×7﹣2×1=35﹣6﹣1.5﹣17.5﹣2=35﹣27=8;
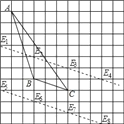
(5)满足条件的 E 点有 8 个,如图,平行于 BC 的直线上,与网格的所有交点即为所求.


科目:初中数学 来源: 题型:
【题目】一点A从数轴上表示+2的点开始移动,第一次先向左移动1个单位,再向右移动2个单位;第二次先向左移动3个单位,再向右移动4个单位;第三次先向左移动5个单位,再向右移动6个单位……
(1)写出第一次移动后这个点在数轴上表示的数为 ;
(2)写出第二次移动后这个点在数轴上表示的数为 ;
(3)写出第五次移动后这个点在数轴上表示的数为 ;
(4)写出第![]() 次移动结果这个点在数轴上表示的数为 ;
次移动结果这个点在数轴上表示的数为 ;
(5)如果第![]() 次移动后这个点在数轴上表示的数为56,求
次移动后这个点在数轴上表示的数为56,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我县各中小学校积极组织学生开展课外阅读活动,为了解某校学生每周课外阅读的时间量t(单位:小时),采用随机抽样的方法抽取部分学生进行了问卷调查,调查结果按0≤t〈2,2≤t〈3,3≤t〈4,t≥4分为四个等级,并分别用A、B、C、D表示.根据调查结果统计数据绘制成如图所示的两幅不完整的统计图,由图中给出的信息解答下列问题:
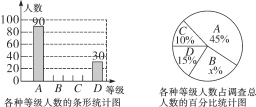
(1)求这次抽查的学生总数是多少人,并求出x的值;
(2)将不完整的条形统计图补充完整;
(3)若该校共有学生3600人,试估计每周课外阅读时间量满足2≤t〈4的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某批发门市销售两种商品,甲种商品每件售价为300元,乙种商品每件售价为80元.新年来临之际,该门市为促销制定了两种优惠方案:
方案一:买一件甲种商品就赠送一件乙种商品;
方案二:按购买金额打八折付款.
某公司为奖励员工,购买了甲种商品20件,乙种商品x(x≥20)件.
(1)分别写出优惠方案一购买费用y1(元)、优惠方案二购买费用y2(元)与所买乙种商品x(件)之间的函数关系式;
(2)若该公司共需要甲种商品20件,乙种商品40件.设按照方案一的优惠办法购买了m件甲种商品,其余按方案二的优惠办法购买.请你写出总费用w与m之间的关系式;利用w与m之间的关系式说明怎样购买最实惠.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,BD、BE分别是高和角平分线,点F在CA的延长线上,FH⊥BE,交BD于点G,交BC于点H;下列结论:①∠DBE=∠F;②2∠BEF=∠BAF+∠C;③∠F=∠BAC-∠C;④∠BGH=∠ABE+∠C,其中正确的结论有___________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,E、F分别为BC、CD的中点,连接AE,BF交于点G,将△BCF沿BF对折,得到△BPF,延长FP交BA延长线于点Q,下列结论正确的个数是( )
①AE=BF;②AE⊥BF;③sin∠BQP= ![]() ;④S四边形ECFG=2S△BGE .
;④S四边形ECFG=2S△BGE . 
A.4
B.3
C.2
D.1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,AB∥CD,点 E 为射线 FG 上一点.
(1)如图 1,若∠EAF=30°,∠EDG=40°,则∠AED= °;
(2)如图 2,当点 E 在 FG 延长线上时,此时 CD 与 AE 交于点 H,则∠AED、∠EAF、∠EDG之间满足怎样的关系,请说明你的结论;
(3)如图 3,DI 平分∠EDC,交 AE 于点 K,交 AI 于点 I,且∠EAI:∠BAI=1:2,∠AED=22°,∠I=20°,求∠EKD 的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB为⊙O的直径,直线l与⊙O相切于点C,AD⊥l,垂足为D,AD交⊙O于点E,连接OC、BE.若AE=6,OA=5,则线段DC的长为 . 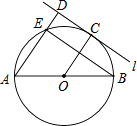
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,点O在对角线AC上,以OA的长为半径的圆O与AD、AC分别交于点E、F,且∠ACB=∠DCE.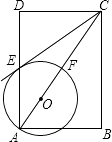
(1)判断直线CE与⊙O的位置关系,并证明你的结论;
(2)若tan∠ACB= ![]() ,BC=2,求⊙O的半径.
,BC=2,求⊙O的半径.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com