
����Ŀ���������عˣ�
�α��о���������λ�����ʵķ���
��֪����ͼ�٣� ��֪![]() �У�
��![]() ��
��![]() �ֱ���
�ֱ���![]() ��
��![]() �����е㣮
�����е㣮
��֤��![]() ��
��![]()
֤�����ӳ�![]() ����
����![]() ��ʹ
��ʹ![]() �� ����
�� ����![]() ����֤��
����֤��![]() ��������
��������
�ɴ˵õ��ı���![]() Ϊƽ���ı��Σ� �����õ���֤����
Ϊƽ���ı��Σ� �����õ���֤����
��1�����������֤�����̣���������������⣺
����ͼ��������֤�����������ĸ����ߣ�����![]() Ǧ���������ߣ���
Ǧ���������ߣ���
����֤������������д���ɣ�����![]() ��
��![]() ��
��![]() ��
��![]() ��ѡ�� .
��ѡ�� .
��������չ��
��2����ͼ�ڣ��ڵȱ�![]() �У� ��
�� ��![]() ������
������![]() ��һ���㣨��
��һ���㣨��![]() �ڵ�
�ڵ�![]() ���Ҳࣩ�����߶�
���Ҳࣩ�����߶�![]() �Ƶ�
�Ƶ�![]() ��ʱ����ת
��ʱ����ת![]() �õ��߶�
�õ��߶�![]() ����
����![]() ���߶�
���߶�![]() ���е㣬����
���е㣬����![]() ��
��![]() ��
��
�������ж��߶�![]() ��
��![]() ��������ϵ��������֤����
��������ϵ��������֤����
����![]() �����߶�
�����߶�![]() ���ȵ���Сֵ��
���ȵ���Сֵ��
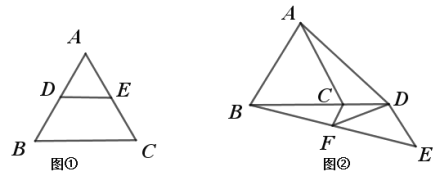
���𰸡��������عˡ���1������ͼ��������֤�����������ĸ����ߣ�����������![]() ����2����
����2����![]() ��֤�������������߶�
��֤�������������߶�![]() ���ȵ���СֵΪ
���ȵ���СֵΪ![]() ��
��
��������
��1���ٸ������⻭���������ɣ�
�������֪�ж�ȫ�ȵ�������![]() ��
��
��2�����ӳ�![]() ����
����![]() ��ʹ��
��ʹ��![]() ������
������![]() ��
��![]() ��֤��
��֤��![]() ���õ�
���õ�![]() ����
����![]() �Ƶ�
�Ƶ�![]() ��ʱ����ת
��ʱ����ת![]() �õ��߶�
�õ��߶�![]() ���ɵõ�
���ɵõ�![]() Ϊ�ȱ������Σ����Ƴ�
Ϊ�ȱ������Σ����Ƴ�![]() Ϊ�ȱ������Σ��õ�
Ϊ�ȱ������Σ��õ�![]() ��
��
������![]() ��ȡ
��ȡ![]() ���е�
���е�![]() ������������
������������![]() ����
����![]() ����������
Ϊ���������Σ�![]() ���õ�
���õ�![]() ���ɵ�
���ɵ�![]() Ϊ
Ϊ![]() ���е㣬��
���е㣬��![]() Ϊ
Ϊ![]() ���е㣬�õ�
���е㣬�õ�![]() ����
����![]() ʱ��
ʱ��![]() ��̣���
��̣���![]() �У�
��![]() ��
��![]() ��
��
��1������ͼ��������֤�����������ĸ�������ͼ��ʾ��
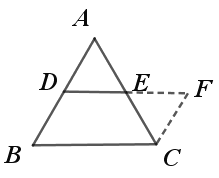
��![]() ��
��
��2����![]() ��
��
�ӳ�![]() ����
����![]() ��ʹ��
��ʹ��![]() ��
��
����![]() ��
��![]() ��
��
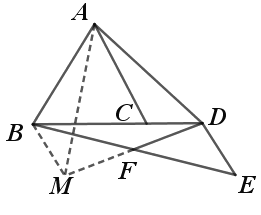
![]() ��
��![]() Ϊ
Ϊ![]() ���е㣬
���е㣬
![]() ��
��
![]() ��
��![]() ��
��
![]() ��
��
![]() ��
��![]() ��
��
![]() ��
��
![]() �Ƶ�
�Ƶ�![]() ��ʱ����ת
��ʱ����ת![]() �õ��߶�
�õ��߶�![]() ��
��
![]() ��
��![]() ��
��
![]() ��
��
![]() Ϊ�ȱ������Σ�
Ϊ�ȱ������Σ�
![]() ��
�� ![]() ��
��
![]() ��
��
![]() ��
��
![]() ��
��
![]() ��
��
![]() ��
��![]() ��
��
![]() ��
��
![]() Ϊ�ȱ������Σ�
Ϊ�ȱ������Σ�
![]() ��
��
������![]() ��ȡ
��ȡ![]() ���е�
���е�![]() ������������
������������![]() ��
��
![]() ����������
����������![]() ��
��
![]() ��
��
![]() ��
��![]() Ϊ
Ϊ![]() ���е㣬��
���е㣬��![]() Ϊ
Ϊ![]() ���е㣬
���е㣬
![]() ��
��
![]() ��
��
![]() ��
��![]() �Ĺ켣Ϊ����
�Ĺ켣Ϊ����![]() ����
����![]() ��
��
��![]() ʱ��
ʱ��![]() ��̣�
��̣�
![]() ��
��
![]() ��
��
��![]() ��
�У�
![]() ��
��
![]() ��
��
���߶�![]() ���ȵ���СֵΪ
���ȵ���СֵΪ![]() ��
��


 ���ѵ����Ԫ��ĩ���100��ϵ�д�
���ѵ����Ԫ��ĩ���100��ϵ�д� ��˼άС�ھ�100����ҵ��ϵ�д�
��˼άС�ھ�100����ҵ��ϵ�д� ��ʦָ��һ��ͨϵ�д�
��ʦָ��һ��ͨϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������������У�����Ͷ�������ڵ�A�����������������˶���·��Ϊ�����ߵ�һ���֣���ͼ1��ʾ����ֱ������ϵ���������߶���Ϊ��B��
��1����������ߵĺ�������ʽ��
��2�������˶�����Cʱ������������CD��x���ڵ�D��CD��2.6m��
����OD�ij���
�ڶ��������������Է�������Ͷ�������ڵ�D����ֱ���������뽫����ֱ�߿��ٴ������ѻ�����Ŀ��Ϊ�����Ľ����E��4��1.3�������������������������߶�h1��m��������ǰ���붫��������ʱ��t��s�����㺯����ϵʽh1����2��t��0.5��2+2.7��0��t��1����С���ڵ�F��1.5��0�������أ����ȶ�����0.3s��ֱ�����������ظ߶�h2��m���붫��������ʱ��t��s���ĺ�����ϵ��ͼ2��ʾ���������������ߵ���״��ͬ����������ֱ�ߴ����ܷ�Խ��С�������ش�����E�����ܣ�����Ӧ��������ʲôʱ�䷶Χ�ڴ��������ܣ���˵�����ɣ�ֱ�ߴ�����������˶�ʱ����Բ��ƣ���
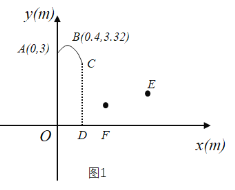

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ�������ĺ�����װ�����������һ��������Щ�����ɫ�ⶼ��ͬ��
��1�������������һ��������ɫ��Żأ��ٴ����������һ����
�������б�������״ͼ�������һ���������ڶ�����������ĸ��ʣ�
����ֱ��д�����������������ɫ�������ɫ�ĸ����� ����
��2�������������һ��������ɫ�Żأ��ٴ����������һ������ֱ��д�����������������ɫ�������ɫ�ĸ����� ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
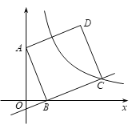
����Ŀ����ͼ����ֱ������ϵ�У�������ABCD�Ƶ�A��0��6����ת������B����x����ʱ����C�պ����ڷ���������![]() ��k��0��x��0)��ͼ���ϣ���֪sin��OAB��
��k��0��x��0)��ͼ���ϣ���֪sin��OAB��![]() .
.
��1�����������ı���ʽ��
��2������������![]() ��ͼ���Ƿ�AD�ߵ��е㣬��˵�����ɣ�
��ͼ���Ƿ�AD�ߵ��е㣬��˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
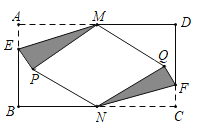
����Ŀ����ͼ�� �ھ���ֽƬ![]() �У�
�� ![]() �� ��
�� ��![]() ��
��![]() �ֱ���
�ֱ���![]() ��
��![]() ���е㣬 ��
���е㣬 ��![]() ��
��![]() �ֱ���
�ֱ���![]() ��
��![]() �ϣ� ��
�ϣ� ��![]() .��
.��![]() ��
��![]() �۵��� ��
�۵��� ��![]() �Ķ�Ӧ��Ϊ��
�Ķ�Ӧ��Ϊ��![]() ����
����![]() ��
��![]() �۵��� ��
�۵��� ��![]() �Ķ�Ӧ��Ϊ��
�Ķ�Ӧ��Ϊ��![]() �����ı���
�����ı���![]() Ϊ����ʱ�� ��
Ϊ����ʱ�� ��![]() _______��
_______��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
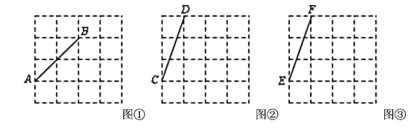
����Ŀ��ͼ�١�ͼ�ڡ�ͼ�۾���4��4������������ÿ��С�����εĶ����Ϊ��㣬С�����εı߳�Ϊ1����![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ���ڸ���ϣ���ͼ�١�ͼ�ڡ�ͼ���У�ֻ���̶ȵ�ֱ�ߣ��ڸ����������а�Ҫ��ͼ������ͼ�εĶ�����ڸ���ϣ���Ҫ��д��������
���ڸ���ϣ���ͼ�١�ͼ�ڡ�ͼ���У�ֻ���̶ȵ�ֱ�ߣ��ڸ����������а�Ҫ��ͼ������ͼ�εĶ�����ڸ���ϣ���Ҫ��д��������
��1����ͼ�������߶�![]() Ϊ��һ��ֱ����
Ϊ��һ��ֱ����![]() ��
��
��2����ͼ�������߶�![]() Ϊ��һ����Գ���
Ϊ��һ����Գ���![]() ��ʹ�����Ϊ5��
��ʹ�����Ϊ5��
��3����ͼ�������߶�![]() Ϊ��һ����Գ��ı���
Ϊ��һ����Գ��ı���![]() ��ʹ�����Ϊ6��
��ʹ�����Ϊ6��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
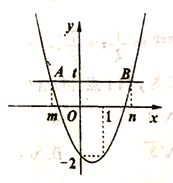
����Ŀ����ͼΪ���κ���![]() ͼ��ֱ��
ͼ��ֱ��![]() �������߽���
�������߽���![]() ����,
����,![]() ���������ֱ�Ϊ
���������ֱ�Ϊ![]() ���ݺ���ͼ����Ϣ�����н���:
���ݺ���ͼ����Ϣ�����н���:
��![]() ;
;
��������![]() ������ֵ����
������ֵ����![]() ,��
,��![]() ;
;
��![]() ;
;
��![]() ;
;
�ݵ�![]() Ϊ��ֵʱ��
Ϊ��ֵʱ��![]() ���,���߶�
���,���߶�![]() �䳤
�䳤
���У���ȷ�Ľ�����__________(д��������ȷ���۵ķ���)
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������![]()
![]() ��
��![]() �ύ��
�ύ��![]() ��
��![]() ���㣬��
���㣬��![]() �ύ�ڵ�
�ύ�ڵ�![]() ����֪��
����֪��![]() ��
��
��1����![]() ����
����![]() ��
��![]() ����Ĺ�ϵʽ��
����Ĺ�ϵʽ��
��2��ֱ��![]() �������߽���
�������߽���![]() ��
��![]() ���㣬�����ߵĶԳ���Ϊֱ��
���㣬�����ߵĶԳ���Ϊֱ��![]() ����
����![]() ��
��
���������ߵĽ���ʽ������ϵ���ú�![]() ��ʽ�ӱ�ʾ����
��ʽ�ӱ�ʾ����
�����߶�![]() ���ȵ�ȡֵ��Χ��
���ȵ�ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
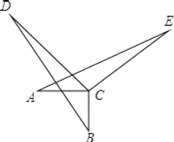
����Ŀ����ͼ��AC��BC��DC��EC��AC=BC��DC=EC��ͼ��AE��BD�������Ĺ�ϵ��������ϵ��λ�ù�ϵ������֤����Ľ��ۣ�
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com