
 x﹣1
x﹣1 ,
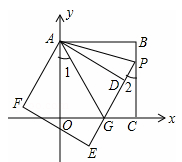
, ,0),CG=3﹣
,0),CG=3﹣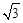 。
。 ,∴P点坐标为:(3,
,∴P点坐标为:(3,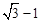 )。
)。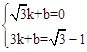 ,解得
,解得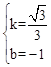 。
。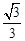 x﹣1。
x﹣1。

 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案科目:初中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 两种型号的学生桌椅500套,以解决1250名学生的学习问题,一套
两种型号的学生桌椅500套,以解决1250名学生的学习问题,一套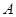 型桌椅(一桌两椅)需木料
型桌椅(一桌两椅)需木料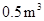 ,一套
,一套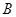 型桌椅(一桌三椅)需木料
型桌椅(一桌三椅)需木料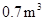 ,工厂现有库存木料
,工厂现有库存木料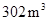 .
.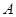 型桌椅的生产成本为100元,运费2元;每套
型桌椅的生产成本为100元,运费2元;每套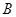 型桌椅的生产成本为120元,运费4元,求总费用
型桌椅的生产成本为120元,运费4元,求总费用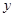 (元)与生产
(元)与生产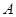 型桌椅
型桌椅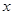 (套)之间的关系式,并确定总费用最少的方案和最少的总费用.(总费用
(套)之间的关系式,并确定总费用最少的方案和最少的总费用.(总费用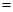 生产成本
生产成本 运费)
运费)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com