
����Ŀ����ͼ��![]() ��
��![]() ƽ��
ƽ��![]() .��һ���㹻������dzߵ�ֱ�Ƕ�����������
.��һ���㹻������dzߵ�ֱ�Ƕ�����������![]() ������һ��
������һ��![]() �ϣ���ʹ���dzߵ�һ��ֱ�DZ���
�ϣ���ʹ���dzߵ�һ��ֱ�DZ���![]() (��
(��![]() ���ӳ���)���ڵ�
���ӳ���)���ڵ�![]() ����һ��ֱ�DZ���
����һ��ֱ�DZ���![]() ���ڵ�
���ڵ�![]() .
.

(1)��ͼ1����![]() ���
���![]() ��ֱʱ��֤��:
��ֱʱ��֤��:![]() ��
��
(2)��ͼ2�������dz��Ƶ�![]() ��ת�����dzߵ�����ֱ�DZ߷ֱ�
��ת�����dzߵ�����ֱ�DZ߷ֱ�![]() �ڵ�
�ڵ�![]() ������ת�����У�
������ת�����У�![]() ��
��![]() �������ֱ��д�����ۣ�
�������ֱ��д�����ۣ�![]()
![]() (��
(��![]() ��
��![]() ��
��![]() )��
)��
(3)��ͼ3�����dz��Ƶ�![]() ������ת�����dzߵ�һ��ֱ�DZ���
������ת�����dzߵ�һ��ֱ�DZ���![]() ���ӳ��߽��ڵ�
���ӳ��߽��ڵ�![]() ����һ��ֱ�DZ���
����һ��ֱ�DZ���![]() ���ڵ�
���ڵ�![]() .����ת�����У�
.����ת�����У�![]() ��
��![]() �����?����ȣ������֤����������ȣ���˵������.
�����?����ȣ������֤����������ȣ���˵������.
���𰸡���1��֤�����̼���������2��������3����ȣ�֤�����̼�����.
��������
��1��֤����DPO����EPO�����ɵó��𰸣�
��2��PD=PE��
��3����PM��ֱAO��M��PN��ֱOB��N��֤����PMD����PNE�����ɵó���.
��1��֤������![]() ��
��![]() ƽ��
ƽ��![]()
���DOP=��POE=45��
�֡�![]() ��
��![]() ���
���![]() ��ֱ
��ֱ
��OE��PD
���POE=��OPD=45��
�֡�DOE=90��
���OPE=45��
����DPO����EPO��

����DPO����EPO��ASA��
��PD=PE
��2��PD=PE
��3��
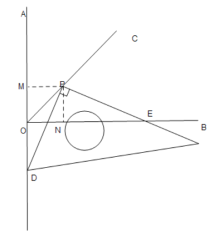
���
֤������PM��ֱAO��M��PN��ֱOB��N
���PMD=��PNE=90��,��MPN=90��
��![]() ƽ��
ƽ��![]()
��PM=PN
�֡�MPN=��MPD+DPN
��DPE=��NPE+��DPN
�ҡ�DPE=90��
���MPD=��NPE
����PMD����PNE��
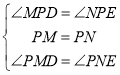
����PMD����PNE��ASA��
��PD=PE
������ת�����У�![]() ��
��![]() ���.
���.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ϸ���ij���й�����������ͬƷ�ֵ�ˮ������һ������2000Ԫ���ڶ�������5500Ԫ���ڶ�������ˮ���������ǵ�һ����2.5�����ҽ��۱ȵ�һ��ÿǧ�˶�1Ԫ��
��1��������ˮ���������˶���ǧ�ˣ�
��2����������ˮ���������������10%������ȫ�����������£����������ˮ�����ۼ���ͬ�����������ʲ�����26%����ô�ۼ����ٶ�Ϊÿǧ�˶���Ԫ��
��������=![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������¥��AB=CD=30m����¥��ľ���AC=24m����̫��������ˮƽ�ߵļн�Ϊ30��ʱ�����¥Ͷ����¥�ϵ�Ӱ�ӵĸ߶ȣ��������ȷ��0.01��![]() ��1.732��
��1.732��![]() ��1.414��
��1.414��
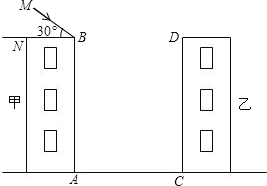
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC�У���ACB��90�㣬AB��5cm��BC��4cm������P�ӵ�A��������ÿ��1cm���ٶ�������A��B��C��A�˶������˶�ʱ��Ϊt��t��0���룮
��1��AC���� ��cm��
��2������Pǡ����AB�Ĵ�ֱƽ�����ϣ����ʱt��ֵ��
��3�����˶������У���tΪ��ֵʱ����ACP����ACΪ���ĵ��������Σ�ֱ��д���������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������������ת����Ϸʱ����ת��A��B�ֱ�ֳ�4�ȷݡ�3�ȷݣ�����ÿһ���ڱ������֣���ͼ��ʾ����Ϸ�涨��ת������ת��ֹͣ��ָ�����ָ��ijһ���֣�������ת��
��1��������״ͼ���б����г����п��ܵĽ����
��2����ָ����ָ���������ֶ��Ƿ���x2-5x+6=0�Ľ�ʱ�����ʤ����ָ����ָ���������ֶ����Ƿ���x2-5x+6=0�Ľ�ʱ�����һ�ʤ������������˭��ʤ�ĸ��ʴ������˵����

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ı���![]() �����Σ��Ե�
�����Σ��Ե�![]() Ϊ����ԭ�㣬
Ϊ����ԭ�㣬![]() ����ֱ��Ϊ
����ֱ��Ϊ![]() �Ὠ��ƽ��ֱ������ϵ������
�Ὠ��ƽ��ֱ������ϵ������![]() ������Ϊ
������Ϊ![]() ��ֱ��
��ֱ��![]() ��
��![]() ���ཻ�ڵ�
���ཻ�ڵ�![]() ������
������![]() ��
��
��1��������![]() �ı߳���
�ı߳���
��2��֤��![]() Ϊֱ�������Σ�
Ϊֱ�������Σ�
��3��ֱ��![]() ���Ƿ����һ��
���Ƿ����һ��![]() ʹ��
ʹ��![]() �������
�������![]() �������ȣ������ڣ��������
�������ȣ������ڣ��������![]() �����ꣻ�������ڣ���˵�����ɣ�
�����ꣻ�������ڣ���˵�����ɣ�


�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�ֱ��AB�뺯��y��![]() ��x��0����ͼ���ڵ�A��m��2����B��2��n��������A��ACƽ����x�ύy���ڵ�C����y�Ḻ������ȡһ��D��ʹOD��
��x��0����ͼ���ڵ�A��m��2����B��2��n��������A��ACƽ����x�ύy���ڵ�C����y�Ḻ������ȡһ��D��ʹOD��![]() OC������ACD�������6������BC��
OC������ACD�������6������BC��
��1����m��k��n��ֵ��
��2������ABC�������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����κ���y��ax2��bx��c��a��0���Ĵ���ͼ����ͼ��ʾ��1��x��h��2��0��xA��1�������н��ۣ��� 2a��b��0���� abc��0���� ��OC��2OA����2b��ac = 4���� 3a��c��0��������ȷ�ĸ����ǣ� ��
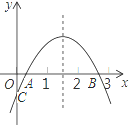
A. 1 B. 2 C. 3 D. 4
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
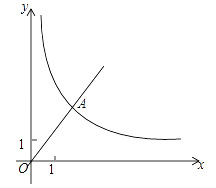
����Ŀ����֪����ͼ����ƽ��ֱ������ϵ�У�����������y=![]() ��ͼ��A����A��������Ϊ4������������y=
��ͼ��A����A��������Ϊ4������������y=![]() ��ͼ��Ҳ������A���ڵ�һ�����ڵĵ�B���������������ͼ���ϣ�����B��BC��x�ᣬ��y���ڵ�C����AC=AB����
��ͼ��Ҳ������A���ڵ�һ�����ڵĵ�B���������������ͼ���ϣ�����B��BC��x�ᣬ��y���ڵ�C����AC=AB����
(1)��������������Ľ���ʽ��
(2)��ABC�����.
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com