
����Ŀ��Ϊ������ij��б��ֻ�����ͬѧ����ʦ���������ľߺ���ֱ���Ϊ��Ʒ����֪5���ľߺС�2֧�ֱʹ���100Ԫ��3���ľߺС�1֧�ֱʹ���57Ԫ��
��1��ÿ���ľߺС�ÿ֧�ֱʸ�����Ԫ��
��2�������α��û����ʦ��������10����Ϊ��Ʒ��������![]() ���ľߺУ�10����Ʒ����
���ľߺУ�10����Ʒ����![]() Ԫ����
Ԫ����![]() ��
��![]() �ĺ�����ϵʽ�����������Ҫ����3���ľߺУ����λ��ʦ�����Ҫ������Ǯ��
�ĺ�����ϵʽ�����������Ҫ����3���ľߺУ����λ��ʦ�����Ҫ������Ǯ��
���𰸡�(1)![]() ;(2) 147Ԫ.
;(2) 147Ԫ.
��������
������ÿ���ľߺ�xԪ��ÿ֧�ֱ�yԪ��Ȼ����ݻ���100Ԫ��57Ԫ�ֱ��г�������ɷ����飬���Ԫһ�η����鼴�ɣ���������������x���ľߺУ���Ʒ����10����������������ľߺкֱʵĵ��ۣ������ܼ۵��ڵ��۳��������õ�һ���ܼ���x֮��ĺ�������ʽ��Ȼ����ݺ��������ʼ��������ֵ.
�����������1����ÿ���ľߺ�xԪ��ÿ֧�ֱ�yԪ��������ã�
![]() ,��֮�ã�
,��֮�ã�![]() .
.
��2��������ã�w="14x+15(10-x)=150-x" ,
��Ϊw��x�������С��![]() ������x=3ʱ��
������x=3ʱ��
W���ֵ=150-3=147������147Ԫ.


 ���ɶ���ܲ��¿�ֱͨ�п�ϵ�д�
���ɶ���ܲ��¿�ֱͨ�п�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����һ�������Ƥ����110cm����70cm���������ĽǸ���ȥһ��ͬ������������Ȼ������ͻ��������������������һ���ǵķ��������Ҫ�������ǵķ��еĵ����Ϊ4500cm2����ô��Ƥ����Ӧ��ȥ�������α߳��Ƕ��٣�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��(1)��ͼ1�У���֪��MAN��120����ACƽ����MAN����ABC����ADC��90�������ܵ������������ۣ��� DC = BC; ��AD+AB=AC.����֤����������
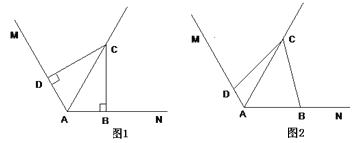
(2)��ͼ2�У��ѣ�1���е���������ABC����ADC��90�㡱��Ϊ��ABC����ADC��180���������������䣬��(1)�еĽ����Ƿ���Ȼ�������������������֤��;������������˵��������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����Rt��ABC��,AB=AC,DΪBC����һ��(�����B,C�غ�),���߶�AD�Ƶ�A��ʱ����ת90��õ�AE.
(1)����EC����ͼ�٣���̽���߶�BC��CD��CE֮������ĵ�����ϵ����֤����Ľ��ۣ�
(2)����DE����ͼ�ڣ���֤��BD2+CD2=2AD2
(3)��ͼ��,���ı���ABCD�У���ABC=��ACB=��ADC=45�㣬��BD=![]() ��CD=1����AD�ij�Ϊ �� .(ֱ��д���𰸣�
��CD=1����AD�ij�Ϊ �� .(ֱ��д���𰸣�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����һ����������ת����ת�̱�ƽ���ֳ�3�����Σ��ֱ����1��2��3�������֣�С����С���ת��һ��ת��Ϊһ����Ϸ����ÿ��ת��ֹͣ��ָ����ָ�����ڵ���Ϊ�������õ�����һ����Ϸ�����õ�һ��������ָ��ָ�ڷֽ���ʱ��ת����

��1����������״ͼ���б��ķ�����ʾ��ÿ����Ϸ���ܳ��ֵ����н����
��2����ÿ����Ϸ�����õ���һ����ǡ���Ƿ���x2-3x+2=0�Ľ�ĸ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����x��һԪ���η���x2����2k+1��x+4k��3=0��
��1����֤������kȡʲôʵ��ֵ���÷���������������ȵ�ʵ������
��2����Rt��ABC��б�߳�aΪ![]() ��������ֱ�DZߵij�b��cǡ����������̵�������ʱ������ABC���ܳ���
��������ֱ�DZߵij�b��cǡ����������̵�������ʱ������ABC���ܳ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ı���ABCD�У���BAD=��C=90�㣬AB=AD��AE��BC��E�����߶�AE=5����S�ı���ABCD=

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����㣺
��![]()
��![]()
��12��7������4����8������2��
��![]()
��33![]()
�ޣ�14��(0.5��2)![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����������y=![]() ��ͼ����һ�κ���y=kx+m��ͼ���ཻ�ڵ�A��2��1����
��ͼ����һ�κ���y=kx+m��ͼ���ཻ�ڵ�A��2��1����
��1���ֱ���������������Ľ���ʽ��
��2����xȡʲô��Χʱ������������ֵ����0��
��3����һ�κ����뷴����������һ����ΪB����������Ϊ��4����xȡʲô��Χʱ������������ֵ����һ�κ�����ֵ��
��4�����жϵ�P����1��5������x��ĶԳƵ�P���Ƿ���һ�κ���y=kx+m��ͼ���ϣ�
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com