
【题目】若关于 ![]() 的一元二次方程
的一元二次方程 ![]() 有两个不相等的实数根,则化简代数式
有两个不相等的实数根,则化简代数式 ![]() 的结果是 .
的结果是 .
【答案】1
【解析】根据方程有两个不相等的实数根可得:4-4×1×(-m)>0,解得:m>-1,则原式= ![]() -
- ![]() =m+2-(m+1)=m+2-m-1=1.
=m+2-(m+1)=m+2-m-1=1.
【考点精析】解答此题的关键在于理解二次根式的性质与化简的相关知识,掌握1、如果被开方数是分数(包括小数)或分式,先利用商的算数平方根的性质把它写成分式的形式,然后利用分母有理化进行化简.2、如果被开方数是整数或整式,先将他们分解因数或因式,然后把能开得尽方的因数或因式开出来,以及对求根公式的理解,了解根的判别式△=b2-4ac,这里可以分为3种情况:1、当△>0时,一元二次方程有2个不相等的实数根2、当△=0时,一元二次方程有2个相同的实数根3、当△<0时,一元二次方程没有实数根.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图1,将一副直角三角尺的顶点叠一起放在点A处,∠BAC=60°,∠DAE=45°,保持三角尺ABC不动,三角尺AED绕点A顺时针旋转,旋转角度小于180°.
(1)如图2,AD是∠EAC的角平分线,直接写出∠DAB的度数;
(2)在旋转的过程中,当∠EAB和∠DAC互余时,求∠BAD的值.
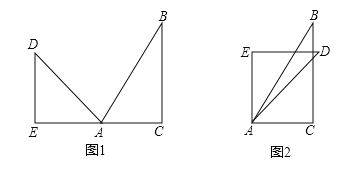
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】布袋中有红、黄、蓝三种不同颜色的球各一个,从中先摸出一个球,记录下颜色后不放回布袋,将布袋搅匀,再摸出一个球,这时摸出的两个球是“一红一黄”的概率为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
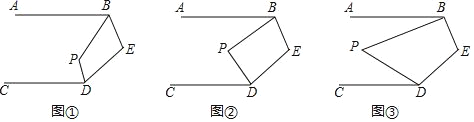
【题目】已知AB∥CD,解决下列问题:
(1)如图①,BP、DP分别平分∠ABE、∠CDE,若∠E=100°,求∠P的度数.
(2)如图②,若∠ABP=![]() ∠ABE,∠CDP=
∠ABE,∠CDP=![]() ∠CDE,试写出∠P与∠E的数量关系并说明理由.
∠CDE,试写出∠P与∠E的数量关系并说明理由.
(3)如图③,若∠ABP=![]() ∠ABE,∠CDP=
∠ABE,∠CDP=![]() ∠CDE,设∠E=m°,求∠P的度数(直接用含n、m的代数式表示,不需说明理由).
∠CDE,设∠E=m°,求∠P的度数(直接用含n、m的代数式表示,不需说明理由).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,AC=BC=4,D是AB的中点,点E、F分别在AC、BC边上运动(点E不与点A、C重合),且保持AE=CF,连接DE,DF,EF.在此运动变化的过程中,有下列结论:
①△DFE是等腰直角三角形;
②四边形CEDF不可能为正方形;
③四边形CEDF的面积随点E位置的改变而发生变化;
④点C到线段EF的最大距离为 ![]() .
.
其中正确结论的个数是( )
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小石和小丁利用盒子里的三张卡片做游戏,卡片上分别写有![]() ,
,![]() ,
,![]() ,这些卡片除了字母外完全相同.从中随机摸出一张卡片记下字母,放回盒子后充分搅匀,再从中随机 摸出一张卡片记下字母.如果两次摸到的卡片字母相同则小石获胜,否则小丁获胜,这个游戏公平吗?请用画树状图或列表的方法说明理由.
,这些卡片除了字母外完全相同.从中随机摸出一张卡片记下字母,放回盒子后充分搅匀,再从中随机 摸出一张卡片记下字母.如果两次摸到的卡片字母相同则小石获胜,否则小丁获胜,这个游戏公平吗?请用画树状图或列表的方法说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知![]() ,
,![]() ,
,![]() 三点在数轴上对应的位置如图如示,其中点
三点在数轴上对应的位置如图如示,其中点![]() 对应的数为2,
对应的数为2,![]() ,
,![]() .
.
![]()
(1)点![]() 对应的数是________,点
对应的数是________,点![]() 对应的数是________;
对应的数是________;
(2)动点![]() ,
,![]() 分别同时从
分别同时从![]() ,
,![]() 两点出发,分别以每秒8个单位和3个单位的速度沿数轴正方向运动.点
两点出发,分别以每秒8个单位和3个单位的速度沿数轴正方向运动.点![]() 为
为![]() 的中点,点
的中点,点![]() 在
在![]() 上,且
上,且![]() ,设运动时间为
,设运动时间为![]() .
.
①请直接用含![]() 的代数式表示点
的代数式表示点![]() ,
,![]() 对应的数;
对应的数;
②当![]() 时,求
时,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某数学兴趣小组将边长为3的正方形铁丝框ABCD变形为以A为圆心,AB为半径的扇形(忽略铁丝的粗细),则所得的扇形DAB的面积为( )
A.6
B.7
C.8
D.9
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若两个扇形满足弧长的比等于它们半径的比,则这称这两个扇形相似。如图,如果扇形AOB与扇形 ![]() 是相似扇形,且半径
是相似扇形,且半径 ![]() (
( ![]() 为不等于0的常数)那么下面四个结论:①∠AOB=∠ A1O1B1
为不等于0的常数)那么下面四个结论:①∠AOB=∠ A1O1B1 ![]() ;②△AOB∽△
;②△AOB∽△ ![]() A1O1B1 ;③
A1O1B1 ;③ ![]() A1B1 =k;④扇形AOB与扇形 A1O1B1
A1B1 =k;④扇形AOB与扇形 A1O1B1 ![]() 的面积之比为
的面积之比为 ![]() 。成立的个数为:( )
。成立的个数为:( )
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com