
【题目】已知:△ABC是一张等腰直角三角形纸板,∠B=90°,AB=BC=1.
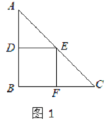
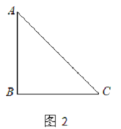
(1)要在这张纸板上剪出一个正方形,使这个正方形的四个顶点都在△ABC的边上.小林设计出了一种剪法,如图1所示.请你再设计出一种不同于图1的剪法,并在图2中画出来.
(2)若按照小林设计的图1所示的剪法来进行裁剪,记图1为第一次裁剪,得到1个正方形,将它的面积记为![]() ,则
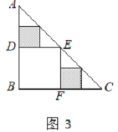
,则![]() =___________;在余下的2个三角形中还按照小林设计的剪法进行第二次裁剪(如图3),得到2个新的正方形,将此次所得2个正方形的面积的和记为
=___________;在余下的2个三角形中还按照小林设计的剪法进行第二次裁剪(如图3),得到2个新的正方形,将此次所得2个正方形的面积的和记为![]() ,则
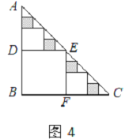
,则![]() =___________;在余下的4个三角形中再按照小林设计的的剪法进行第三次裁剪(如图4),得到4个新的正方形,将此次所得4个正方形的面积的和记为
=___________;在余下的4个三角形中再按照小林设计的的剪法进行第三次裁剪(如图4),得到4个新的正方形,将此次所得4个正方形的面积的和记为![]() ;按照同样的方法继续操作下去……,第
;按照同样的方法继续操作下去……,第![]() 次裁剪得到_________个新的正方形,它们的面积的和
次裁剪得到_________个新的正方形,它们的面积的和![]() =______________.
=______________.
【答案】(1)画图见解析;(2)(2)![]() ,
,![]() ,
,![]() ,
,![]() .
.
【解析】(1)利用斜边长的![]() ,向斜边作垂线得出正方形即可;
,向斜边作垂线得出正方形即可;
(2)根据题意,可求得S1,S2,S3,同理可得规律:Sn即是第n次剪取后面积和,根据此规律求解即可答案.
(1)如图所示;
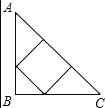
(2)∵四边形DBFE是正方形,
∴DE=EF=BF=DB,∠EFC=∠ADE=90°,
∵△ABC是等腰直角三角形,
∴∠A=∠C=45°,
∴AD=DE=EF=CF=BF=BD,
∵AB=BC=1,
∴DE=EF=![]() ,
,
∴S正方形DBFE=S1=![]() ×
×![]() =
=![]() ;
;
同理:S2即是第二次剪取后的面积和,
Sn即是第n次剪取后的面积和,
∴第一次剪取后的面积和为:S1=![]() =
=![]() ,
,
第二次剪取后的面积和为:S2=![]() ×
×![]() ×2=
×2=![]() =
=![]() ,
,
第三次剪取后剩余三角形面积和为:S3=![]() ×
×![]() ×4=
×4=![]() =
=![]() ,
,
…
第n次剪取后面积和为:Sn=![]() ×
×![]() ×2n1=
×2n1=![]() .
.
故答案为:![]() ,
,![]() ,2n1,
,2n1,![]() .
.


科目:初中数学 来源: 题型:
【题目】(本小题满分9分)如图,四边形ABCD中AB∥CD,AB≠CD,BD=AC。
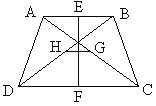
(1)求证:AD=BC;
(2)若E,F,G,H分别是AB,CD,AC,BD的中点,求证:线段EF与线段GH互相垂直平分。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y= ![]() x2﹣2x﹣6
x2﹣2x﹣6 ![]() 与x轴交于A,B两点(点A在点B左侧),与y轴交于点C,点D为顶点,点E在抛物线上,且横坐标为4
与x轴交于A,B两点(点A在点B左侧),与y轴交于点C,点D为顶点,点E在抛物线上,且横坐标为4 ![]() ,AE与y轴交F.
,AE与y轴交F.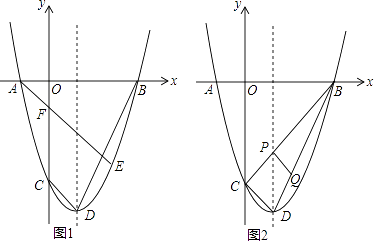
(1)求抛物线的顶点D和F的坐标;
(2)点M,N是抛物线对称轴上两点,且M(2 ![]() ,a),N(2
,a),N(2 ![]() ,a+
,a+ ![]() ),是否存在a使F,C,M,N四点所围成的四边形周长最小,若存在,求出这个周长最小值,并求出a的值;
),是否存在a使F,C,M,N四点所围成的四边形周长最小,若存在,求出这个周长最小值,并求出a的值;
(3)连接BC交对称轴于点P,点Q是线段BD上的一个动点,自点D以2 ![]() 个单位每秒的速度向终点B运动,连接PQ,将△DPQ沿PQ翻折,点D的对应点为D′,设Q点的运动时间为t(0≤t≤
个单位每秒的速度向终点B运动,连接PQ,将△DPQ沿PQ翻折,点D的对应点为D′,设Q点的运动时间为t(0≤t≤ ![]() )秒,求使得△D′PQ与△PQB重叠部分的面积为△DPQ面积的
)秒,求使得△D′PQ与△PQB重叠部分的面积为△DPQ面积的 ![]() 时对应的t值.
时对应的t值.
查看答案和解析>>
科目:初中数学 来源: 题型:
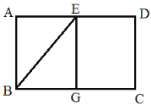
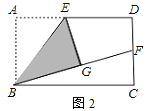
【题目】如图,在矩形ABCD中,E是AD的中点,将△ABE沿BE折叠,点A的对应点为点G.
(1)填空:如图1,当点G恰好在BC边上时,四边形ABGE的形状是___________形;
(2)如图2,当点G在矩形ABCD内部时,延长BG交DC边于点F.
![]() 求证:BF=AB+DF;
求证:BF=AB+DF;
![]() 若AD=
若AD=![]() AB,试探索线段DF与FC的数量关系.
AB,试探索线段DF与FC的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=x2﹣mx﹣3(m>0)交y轴于点C,CA⊥y轴,交抛物线于点A,点B在抛物线上,且在第一象限内,BE⊥y轴,交y轴于点E,交AO的延长线于点D,BE=2AC.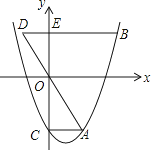
(1)用含m的代数式表示BE的长.
(2)当m= ![]() 时,判断点D是否落在抛物线上,并说明理由.
时,判断点D是否落在抛物线上,并说明理由.
(3)若AG∥y轴,交OB于点F,交BD于点G.
①若△DOE与△BGF的面积相等,求m的值.
②连结AE,交OB于点M,若△AMF与△BGF的面积相等,则m的值是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等边三角形纸片ABC中,点D在边AB(不包含端点A、B)上运动,连接CD,将∠ADC对折,点A落在直线CD上的点A′处,得到折痕DE;将∠BDC对折,点B落在直线CD上的点B′处,得到折痕DF.
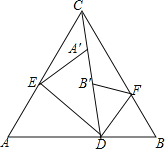
(1)若∠ADC=80°,求∠BDF的度数;
(2)试问∠EDF的大小是否会随着点D的运动而变化?若不变,求出∠EDF的大小;若变化,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
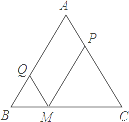
【题目】已知:△ABC中AB=AC,M为底边BC上任意一点,过点M分别作AB、AC的平行线交AC于P,交AB于Q.
探究:(1)线段QM、PM、AB之间有什么关系?并说明你的理由.
(2)当M位于BC的什么位置时, 四边形AQMP是菱形?并说明你的理由.
(3)当△ABC满足什么条件菱形AQMP是正方形?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com