练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    分解因式：            .


    y(x-2)

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：


     如图，试沿着虚线把图形分成两个全等图形.

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    已知关于的函数图象如图所示，则当时，自变量的取值范围是（    ）

    A、                    B、或

    C、                   D、或

     


    查看答案和解析>>

    科目：初中数学 来源： 题型：


    观察控究，完成证明和填空．

    如图，四边形ABCD中，点E、F、G、H分别是边AB、BC、CD、DA的中点，顺次连接E、F、G、H，得到的四边形EFGH叫中点四边形．

    （1）求证：四边形EFGH是平行四边形；

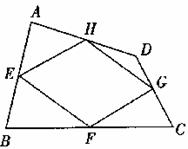
    （2）如图，当四边形ABCD变成等腰梯形时，它的中点四边形是菱形，请你探究并填空：

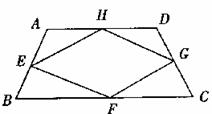
    当四边形ABCD变成平行四边形时，它的中点四边形是＿＿＿＿＿＿＿＿＿＿；

    当四边形ABCD变成矩形时，它的中点四边形是＿＿＿＿＿＿＿＿＿＿；

    当四边形ABCD变成菱形时，它的中点四边形是＿＿＿＿＿＿＿＿＿＿；

    当四边形ABCD变成正方形时，它的中点四边形是＿＿＿＿＿＿＿＿＿＿；

    （3）根据以上观察探究，请你总结中点四边形的形状由原四边形的什么决定的？

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    已知圆锥的侧面展开图的圆心角为120°，则这个圆锥的侧面积是底面积的（   ）

    A．2倍          B．3倍           C．             D．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    古希腊数学家把数1,3,6,10,15,21，……叫做三角形数，它有一定的规律性，若把第一个三角形数记为a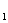,第二个三角数形记为a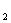,……，第n个三角形数记为a,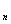

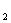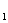    计算a－ a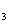,a－ a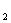……由此推算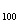a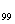－a=         a=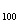        

                                       

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    随着人民生活水平的不断提高，萧山区家庭轿车的拥有量逐年增加.据统计，家景园小区2008年底拥有家庭轿车144辆，2010年底家庭轿车的拥有量达到225辆.

    （1）     若该小区2008年底到2010年底家庭轿车拥有量的年平均增长率都相同，求该小区到2011年底家庭轿车将达到多少辆？

    （2）     为了缓解停车矛盾，该小区决定投资25万元再建造若干个停车位.据测算，建造费用分别为室内车位6000元/个，露天车位2000元/个，考虑到实际因素，计划露天车位的数量不少于室内车位的3倍，但不超过室内车位的4.5倍，求该小区最多可建两种车位各多少个？试写出所有可能的方案.

    查看答案和解析>>

    科目：初中数学 来源： 题型：


     正方形A1B1C1O，A2B2C2C1，A3B3C3C2，…按如图所示的方式放置．点A1，A2，A3，…和点C1，C2，C3，…分别在直线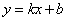(k＞0)和x轴上，已知点B1(1，1)，B2(3，2)，则Bn的坐标是_____  _________．

     


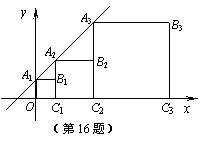    查看答案和解析>>

    科目：初中数学 来源： 题型：


    函数在同一直角坐标系内的图象大致是（   ）

    查看答案和解析>>

    同步练习册答案