
����Ŀ�����о��С���ʮ�߽���Сѧ���鷨��������Ʒ��������֪ÿ��������Ʒ�ɼ���Ϊ![]() ����ί���1000���鷨��Ʒ�������ȡ�˲��ֲ�����Ʒ��ͳ�������ǵijɼ��������Ƴ�����ͳ��ͼ����
����ί���1000���鷨��Ʒ�������ȡ�˲��ֲ�����Ʒ��ͳ�������ǵijɼ��������Ƴ�����ͳ��ͼ����
������ | Ƶ�� | �ٷֱ� |
| 38 | 0.38 |
| ________ | 0.32 |
| ________ | ________ |
| 10 | 0.1 |
�ϼ� | ________ | 1 |

����������Ϣ������������⣺
��1������鷨��Ʒ�����ɼ��ĵ����Dz���_____����ղ顱�������顱����������_____��
��2������ϱ�������ȫ�鷨��Ʒ�����ɼ�Ƶ��ֱ��ͼ��
��3����80�֣���80�֣����ϵ��鷨��Ʒ������Ϊ�ȼ������Թ���ȫ�л�õȼ�����������
���𰸡���1���������飻100���鷨��Ʒ����2��32��20��0.2����3��300��.
��������
��1�����������֪����1000����Ʒ�г�ȡ��100�������ڳ������飬���ɵõ��𰸣��ٸ��ݷ�������60��x��70Ƶ����Ƶ�����������
��2����60��x��70Ƶ����Ƶ���������������Ƶ��=Ƶ�����������Ƶ����Ƶ�ʼ��ɣ������������ݲ�ȫͼ�μ��ɵã�
��3����������80�����ϵİٷֱȼ��ɣ�
�⣺��1���������⣬��ί���1000���鷨��Ʒ�������ȡ�˲��ֲ�����Ʒ��ͳ�������ǵijɼ���֪������鷨��Ʒ�����ɼ��ĵ����Dz��ó������飻
����������![]() ��
��
�������ǣ�100���鷨��Ʒ�ı����ɼ���
�ʴ�Ϊ���������飬100���鷨��Ʒ�ı����ɼ���
��2���ѱ������������±���

�ʴ�Ϊ�� 32��20��100��0.2��
��ȫ�鷨��Ʒ�����ɼ�Ƶ��ֱ��ͼ��ͼ��ʾ��

��3��1000����0.2+0.1��=300��������
��ȫ�л�õȼ����ķ���Ϊ300����


 ��У����ϵ�д�
��У����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1����֪ƽ���ı���ABCD����A������Ϊ��2��6������B��y���ϣ���AD��BC��x�ᣬ��B��C��D�����������y=ax2+bx+c��a��0���Ķ�������Ϊ��2��2������F��m��6�����߶�AD��һ���㣬ֱ��OF��BC�ڵ�E��
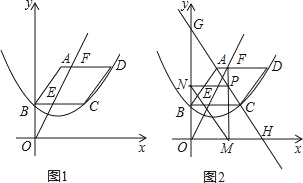
��1���������ߵı���ʽ��
��2�����ı���ABEF�����ΪS�������S��m�ĺ�����ϵʽ����д���Ա���m��ȡֵ��Χ��
��3����ͼ2������F��FM��x�ᣬ����ΪM����ֱ��AC��P������P��PN��y�ᣬ����ΪN������MN��ֱ��AC�ֱ�x�ᣬy���ڵ�H��G�������߶�MN����Сֵ����ֱ��д����ʱm��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������֪�������Ե������������Ρ������λ����������������棬�������Ҫͬʱ�����ֲ�ͬ����������������棬������Ƴ����ֲ�ͬ����Ϸ�����
��������
����1���Ƿ����ͬʱ�������Ρ����˱������������������������棿
��֤1�������գ����̵���ʱ����Χ��ijһ������x�������κ�y�����˱��ε��ڽǿ���ƴ��һ���ܽǣ��������⣺�ɵ÷��̢٣� ��
�����âڣ� ��
���ǿ����ҵ����̵���������Ϊ�ۣ� ��
����1����������ʱ����һ��������ΧΧ���Ţܸ������κ͢ݸ����˱��ε��ڽǿ���ƴ��һ���ܽǣ�����ͬʱ�������κ����˱����������������Ͽ����������森
����2���Ƿ����ͬʱ���������κ������������������������������棿���ܣ��밴����������������֤����д�����п��ܵķ����������ܣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij���ճ������һ��ɱ�Ϊ10Ԫ/���Ĺ���ƷͶ���г�����������
�������飬�õ��������ݣ�
���۵���x��Ԫ/���� | �� | 20 | 30 | 40 | 50 | 60 | �� |
ÿ��������y������ | �� | 500 | 400 | 300 | 200 | 100 | �� |
��1�����ϱ���x��y�ĸ����Ӧֵ��Ϊ������꣬�������ƽ��ֱ������ϵ�������Ӧ�ĵ㣬����y��x�ĺ�����ϵʽ�������������ϵʽ��
��2����۲��Ź涨���ù���Ʒ�����۵�����߲�����45Ԫ/���������۵���x��Ϊ����ʱ�����ճ������ù���Ʒÿ���õ�����8000Ԫ��������=�����ܼ۩��ɱ��ܼۣ�
��3�������۵��۶�Ϊ����ʱ�����ճ������ù���Ʒÿ���õ����������������Ƕ��٣�������=�����ܼ۩��ɱ��ܼۣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������y=![]() x2��
x2��![]() x��9��x�ύ��A��B���㣬��y�ύ�ڵ�C������BC��AC��
x��9��x�ύ��A��B���㣬��y�ύ�ڵ�C������BC��AC��
��1����AB��OC�ij���
��2����E�ӵ�A��������x�����B�˶�����E���A��B���غϣ�������E��ֱ��lƽ��BC����AC�ڵ�D����AE�ij�Ϊm����ADE�����Ϊs����s����m�ĺ�����ϵʽ����д���Ա���m��ȡֵ��Χ��
��3���ڣ�2���������£�����CE������CDE��������ֵ����ʱ������Ե�EΪԲ�ģ���BC���е�Բ��������������������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�������![]() �У�
��![]() ��
��![]() ���ϵĸ�.
���ϵĸ�. ![]() ,��
,��![]()
![]() .����
.����![]() ����
����![]() ���ӳ����ڵ�
���ӳ����ڵ�![]() ������
������![]() .�����:��
.�����:��![]() ;��
;��![]() ;��
;��![]() ;��
;��![]() .����һ����ȷ�ĸ����ǣ� ��
.����һ����ȷ�ĸ����ǣ� ��

A.![]() ��B.
��B.![]() ��
��
C.![]() ��D.
��D.![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ�������������У���ABC�Ķ�����ڸ���ϣ���������ֱ������ϵ�а�Ҫ��ͼ�ͽ���������⣺
(1)����ABC��x�ᷭ�ۺ�����x������ƽ��1����λ����ͼ�л���ƽ�ƺ�ġ�A1B1C1��
(2)����ABC����һ��P��a,b��������1���е����α任���P�������Ϊ_____________
(3)������ABC��������ԭ��O�����ĶԳƵġ�A2B2C2��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������AEFG�Ķ���E��G�ֱ���������ABCD��AB��AD���ϣ�����B����EF�ڵ�M����FG�ڵ�N����AE=a��AG=b��AB=c��b��a��c����
��1����֤�� ![]() ��
��
��2������AMN���������a��b��c�Ĵ���ʽ��ʾ����
��3������MAN=45��ʱ����֤��c2=2ab��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����������ABCD�У�AF=BE��AE��DF�ཻ�ڵ�O��

��1����֤����DAF�ա�ABE��
��2��д���߶�AE��DF��������λ�ù�ϵ����˵�����ɣ�
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com