
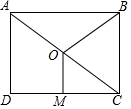
 如图,点O是矩形ABCD的对角线AC的中点,M是CD边的中点.若AB=8,OM=3,则线段OB的长为5.
如图,点O是矩形ABCD的对角线AC的中点,M是CD边的中点.若AB=8,OM=3,则线段OB的长为5.  天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
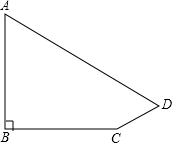 如图,学校旗杆附近有一斜坡,小明准备测量学校旗杆AB的高度,他发现当斜坡正对着太阳时,旗杆AB的影子恰好落在水平地面和斜坡的坡面上,此时小明测得水平地面上的影长BC=16米,斜坡坡面上的影长CD=4米,太阳光线AD与水平地面成30°角,斜坡CD与水平地面BC成30°的角.求旗杆AB的高度.($\sqrt{3}$=1.732,精确到1米)
如图,学校旗杆附近有一斜坡,小明准备测量学校旗杆AB的高度,他发现当斜坡正对着太阳时,旗杆AB的影子恰好落在水平地面和斜坡的坡面上,此时小明测得水平地面上的影长BC=16米,斜坡坡面上的影长CD=4米,太阳光线AD与水平地面成30°角,斜坡CD与水平地面BC成30°的角.求旗杆AB的高度.($\sqrt{3}$=1.732,精确到1米)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
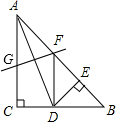 如图,在△ABC中,AC=BC=2,∠C=90°,AD是△ABC的角平分线,DE⊥AB,垂足为E,AD的垂直平分线交AB于点F,则DF的长为4-2$\sqrt{2}$.
如图,在△ABC中,AC=BC=2,∠C=90°,AD是△ABC的角平分线,DE⊥AB,垂足为E,AD的垂直平分线交AB于点F,则DF的长为4-2$\sqrt{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
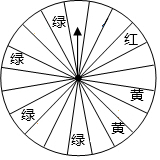 某商场为了吸引顾客,设立了一个可以自由转动的转盘(转盘被等分成20个扇形,如图)并规定:顾客在本商场每消费200元,就能获得一次转动转盘的机会,如果转盘停止后,指针正好对准红、黄或绿色区域,顾客就可以分别获得100元、50元、20元的购物券.某顾客消费210元,他转动转盘获得购物券的概率是多少?他得到100元、50元、20元购物券的概率分别是多少?
某商场为了吸引顾客,设立了一个可以自由转动的转盘(转盘被等分成20个扇形,如图)并规定:顾客在本商场每消费200元,就能获得一次转动转盘的机会,如果转盘停止后,指针正好对准红、黄或绿色区域,顾客就可以分别获得100元、50元、20元的购物券.某顾客消费210元,他转动转盘获得购物券的概率是多少?他得到100元、50元、20元购物券的概率分别是多少?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com