
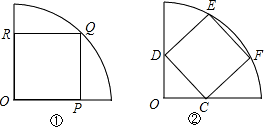
如图,在半径为2的扇形AOB中,∠AOB=90°,点C是弧AB上的一个动点(不与点A、B重合)OD⊥BC,OE⊥AC,垂足分别为D、E.
(1)当BC=1时,求线段OD的长;
(2)在△DOE中是否存在长度保持不变的边?如果存在,请指出并求其长度,如果不存在,请说明理由;
(3)设BD=x,△DOE的面积为y,求y关于x的函数关系式,并写出x的取值范围.

解:(1)如图(1),∵OD⊥BC∴BD=BC=,………………………………2分
∴OD=![]() =
=![]() ;………………………………………………………………4分
;………………………………………………………………4分



(2)如图(2),存在DE是不变的.…………………………………………… 5分
连接AB,则AB=![]() =2
=2![]() ,…………………………………………6分
,…………………………………………6分
∵D和E是中点,
∴DE=AB=![]() ;………………………………………………………………8分
;………………………………………………………………8分
(3)如图(3),∵BD=x,∴OD=![]() ……………………………………9分
……………………………………9分
∵∠1=∠2,∠3=∠4,∴∠2+∠3=45°,……………………………………10分
过D作DF⊥OE.∴DF=![]() ,EF=
,EF=![]() x,………………………………11分
x,………………………………11分
∴y=DF•OE=![]() ···················· 13分
···················· 13分
(0<x<![]() ).··························· 14分
).··························· 14分


 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com