
【题目】已知:△AOB和△COD均为等腰直角三角形,∠AOB=∠COD=90°.连接AD,BC,点H为BC中点,连接OH.
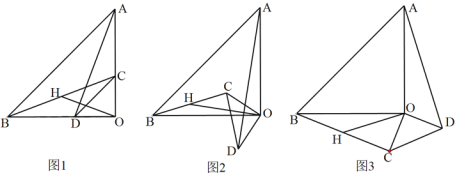
(1)如图1所示,求证:![]() 且
且![]()
(2)将△COD绕点O旋转到图2、图3所示位置时,线段OH与AD又有怎样的关系,并选择一个图形证明你的结论
【答案】(1)详见解析;(2)详见解析.
【解析】
(1)首先证明△AOD≌△BOC(SAS),利用全等三角形的性质得到BC=AD,再利用直角三角形斜边中线的性质即可得到OH=![]() BC=
BC=![]() AD,然后通过全等三角形对应角相等以及直角三角形两锐角互余证明OH⊥AD;
AD,然后通过全等三角形对应角相等以及直角三角形两锐角互余证明OH⊥AD;
(2)如图2中,延长OH到E,使得HE=OH,连接BE,通过证明△BEO≌△ODA,可得OH=![]() OE=
OE=![]() AD以及∠DAO+∠AOH=∠EOB+∠AOH=90°,问题得证;如图3中,延长OH到E,使得HE=OH,连接BE,延长EO交AD于G,同理可证OH=
AD以及∠DAO+∠AOH=∠EOB+∠AOH=90°,问题得证;如图3中,延长OH到E,使得HE=OH,连接BE,延长EO交AD于G,同理可证OH=![]() OE=
OE=![]() AD,∠DAO+∠AOG=∠EOB+∠AOG=90°.
AD,∠DAO+∠AOG=∠EOB+∠AOG=90°.
(1)证明:如图1中,∵△OAB与△OCD为等腰直角三角形,∠AOB=∠COD=90°,

∴OC=OD,OA=OB,
在△AOD与△BOC中,
∵OA=OB,∠AOD=∠BOC,OD=OC,
∴△AOD≌△BOC(SAS),
∴BC=AD
∵H是BC中点,
∴OH=![]() BC=
BC=![]() AD.
AD.
∵△AOD≌△BOC
∴∠ADO=∠BCO,∠OAD=∠OBC,
∵点H为线段BC的中点,
∴∠OBH=∠HOB=∠OAD,
又∵∠OAD+∠ADO=90°,
∴∠ADO+∠BOH=90°,
∴OH⊥AD;
(2)解:结论:OH⊥AD,OH=![]() AD
AD

证明:如图2中,延长OH到E,使得HE=OH,连接BE,
易证△BEO≌△ODA,
∴OE=AD,∴OH=![]() OE=
OE=![]() AD.
AD.
由△BEO≌△ODA,知∠EOB=∠DAO,
∴∠DAO+∠AOH=∠EOB+∠AOH=90°,
∴OH⊥AD.
如图3中,结论不变.延长OH到E,使得HE=OH,连接BE,延长EO交AD于G.
易证△BEO≌△ODA,

∴OE=AD,∴OH=![]() OE=
OE=![]() AD.
AD.
由△BEO≌△ODA,知∠EOB=∠DAO,
∴∠DAO+∠AOG=∠EOB+∠AOG=90°,
∴∠AGO=90°,
∴OH⊥AD.


科目:初中数学 来源: 题型:
【题目】某商场销售一款西服和领带,西服每套定价600元,领带每条定价80元,该商场在周末开展促销活动,向顾客提供两种优惠方案:①买一套西服送一条领带;②西服和领带都按定价 的90%付款.现某客户要购买西服20套,领带![]() 条(
条(![]() )
)
(1)若该客户按方案①购买,需付款多少元? (用含![]() 的代数式表示)
的代数式表示)
(2)若该客户按方案②购买,需付款多少元?(用含![]() 的代数式表示)
的代数式表示)
(3)若![]() ,通过计算说明此时按哪种方案购买较为合算?
,通过计算说明此时按哪种方案购买较为合算?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,∠B=60°,BC=2,△A′B′C可以由△ABC绕点C顺时针旋转得到,其中点A′与点A是对应点,点B′与点B是对应点,连接AB′,且A、B′、A′在同一条直线上,则AA′的长为( )

A. 6 B. 4![]() C. 3
C. 3![]() D. 3
D. 3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】暑假期间,小明和父母一起开车到距家200千米的景点旅游.出发前,汽车油箱内储油45升,当行驶150千米时,发现油箱剩余油量为30升.(假设行驶过程中汽车的耗油量是均匀的.)
(1)写出用行驶路程x(千米)来表示剩余油量Q(升)的代数式;
(2)当x=300千米时,求剩余油量Q的值;
(3)当油箱中剩余油量少于3升时,汽车将自动报警.如果往返途中不加油,他们能否在汽车报警前回到家?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
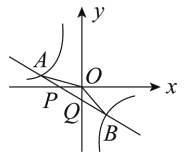
【题目】如图,已知直线![]() 与
与![]() 轴、
轴、![]() 轴相交于
轴相交于![]() 、
、![]() 两点,与
两点,与![]() 的图象相交于
的图象相交于![]() 、
、![]() 两点,连接
两点,连接![]() 、
、![]() .给出下列结论:
.给出下列结论:
①![]() ;②
;②![]() ;③
;③![]() ;④不等式
;④不等式![]() 的解集是
的解集是![]() 或
或![]() .
.
其中正确结论的序号是__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市某中学计划购进若干个甲种规格的排球和乙种规格的足球. 如果购买20个甲种规格的排球和15个乙种规格的足球,一共需要花费2050元;如果购买10个甲种规格的排球和20个乙种规格的足球,一共需要花费1900元。
(1)求每个甲种规格的排球和每个已汇总规格的足球的价格分别是多少元?
(2)如果学校要购买甲种规格的排球和乙种规格的足球共50个,并且预算总费用不超过3080元,那么该学校至多能购买多少个乙种规格的足球?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com