练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，方格纸中的每个小方格都是边长为1个单位的正方形，在建立平面直角坐标系后，点A、B、C均在格点上．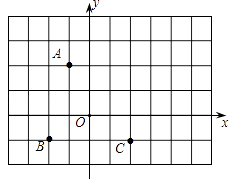

    （1）请直接写出点A、B、C的坐标；
    （2）若平移线段AB，使B移动到C的位置，请在图中画出A移动后的位置D，依次连接B、C、D、A，并求出四边形ABCD的面积．

    【答案】
    （1）

    解：A（﹣1，2），B（﹣2，﹣1），C（2，﹣1）


    （2）

    解：画图如下：

    四边形ABCD的面积=4×3=12．


    【解析】（1）利用坐标系，根据各点所在象限的符号和距坐标轴的距离可得各点的坐标；（2）因为平移线段AB，使B移动到C的位置，所以A需相应的向右平移4格，即可作出图形，根据对应线段平行且相等可知这是一个平行四边形，利用简单计算即可求出其面积．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】已知抛物线y=ax2+bx+3的对称轴是直线x=1．

    （1）求证：2a+b=0；

    （2）若关于x的方程ax2+bx﹣8=0的一个根为4，求方程的另一个根．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】抛物线（）的对称轴为直线，与x轴的一个交点A在点和之间，其部分图象如图，则下列4个结论：①；②2ab=0；③；④点M（， ）、N（， ）在抛物线上，若，

    则，其中正确结论的个数是（ ）.

    A. 1个 B. 2个 C. 3个 D. 4个

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某公司员工的月工资如下表：

    则这组数据的平均数、众数、中位数分别为（　　）.
    A.2200元、1800元、1600元
    B.2000元、1600元、1800元
    C.2200元、1600元、1800元
    D.1600元、1800元、1900元

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在平面直角坐标系中，A（1，1），B（﹣1，1），C（﹣1，﹣2），D（1，﹣2），把一条长为2016个单位长度且没有弹性的细线（线的粗细忽略不计）的一端固定在点A处，并按A→B→C→D→A…的规律绕在四边形ABCD的边上，则细线另一端所在位置的点的坐标是（ ）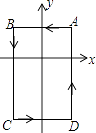

    A.（﹣1，0）
    B.（1，﹣2）
    C.（1，1）
    D.（0，﹣2）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】甲、乙、丙三人之间相互传球，球从一个人手中随机传到另外一个人手中，共传球三次．

    （1）若开始时球在甲手中，求经过三次传球后，球传回甲手中的概率是多少？

    （2）若丙想使球经过三次传递后，球落在自己手中的概率最大，丙会让球开始时在谁手中？请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知AB∥CD，分别探究下面两个图形中∠APC和∠PAB、∠PCD的关系，请从你所得两个关系中选出任意一个，说明你探究的结论的正确性．
    结论：
    （1）
    （2） 选择结论： ， 说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在平面直角坐标系中，△ABC三个顶点的坐标分别为A（﹣4，﹣1）、B（﹣2，3）、C（2，0），将△ABC先向右平移5个单位，再向上平移3个单位，得到△A1B1C1 ．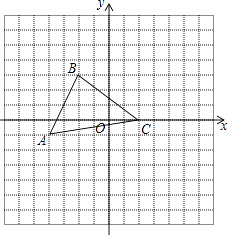

    （1）画出△A1B1C1；
    （2）写出点A1 ， B1 ， C1的坐标．
    （3）求△ABC的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知直线AB、CD被直线EF所截，FG平分∠EFD，∠1=∠2=80°，求∠BGF的度数． 解：因为∠1=∠2=80°（已知），
    所以AB∥CD（）
    所以∠BGF+∠3=180°（）
    因为∠2+∠EFD=180°（邻补角的性质）．
    所以∠EFD= ． （等式性质）．
    因为FG平分∠EFD（已知）．
    所以∠3=∠EFD（角平分线的性质）．
    所以∠3= ． （等式性质）．
    所以∠BGF= ． （等式性质）．

    查看答案和解析>>

    同步练习册答案