
| DF |
| CG |
| DF |
| CG |
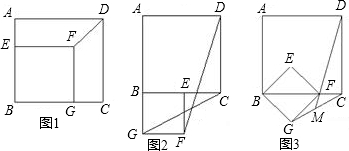
| DF |
| CG |
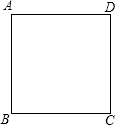
| 2 |
| 2 |
| 2 |
| 2 |
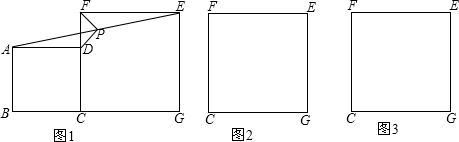
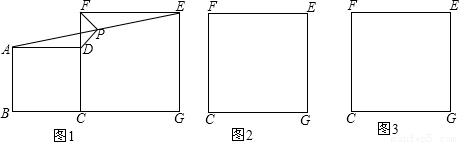
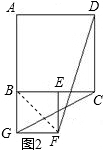 解:(1)如图2,连接BF,
解:(1)如图2,连接BF,| 2 |
| 2 |
| FD |
| CG |
| BF |
| BG |
| DF |
| CG |
| 2 |
| 2 |
| 2 |
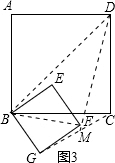
| DF |
| CG |
| 2 |
| DF |
| CG |
| 2 |


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
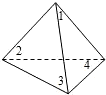
 (一)如图,放在直角坐标系中的正方形ABCD的边长为4.现做如下实验:
(一)如图,放在直角坐标系中的正方形ABCD的边长为4.现做如下实验:| 3 | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:
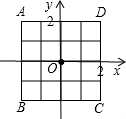 如图,放在直角坐标系中的正方形ABCD边长为4,现做如下实验:抛掷一枚均匀的正四面体骰子(它有四个顶点,各顶点的点数分别是1至4这四个数字中一个),每个顶点朝上的机会是相同的,连续抛掷两次,将骰子朝上的顶点数作为直角坐标中P点的坐标)第一次的点数作横坐标,第二次的点数作纵坐标).
如图,放在直角坐标系中的正方形ABCD边长为4,现做如下实验:抛掷一枚均匀的正四面体骰子(它有四个顶点,各顶点的点数分别是1至4这四个数字中一个),每个顶点朝上的机会是相同的,连续抛掷两次,将骰子朝上的顶点数作为直角坐标中P点的坐标)第一次的点数作横坐标,第二次的点数作纵坐标).| 3 | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源:2010年中考数学模拟卷(2)(解析版) 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com