Question

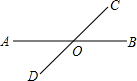
直线AB，CD相交于点O，∠BOC=40°．
（1）写出∠BOC的邻补角；（2）求∠AOC，∠AOD，∠BOD度数．

Answer 1

解：（1）∠BOC的邻补角是∠BOD与∠AOC．

（2）∵∠BOC=40°，
∴∠AOD=∠BOC=40°，
∵∠BOC+∠AOC=180°，
∴∠AOC=180°-∠BOC=180°-40°=140°，
∴∠BOD=∠AOC=140°，
∴∠AOC、∠AOD、∠BOD的度数分别为140°、40°、140°．
分析：（1）根据邻补角的概念可求∠BOC的邻补角是∠BOD与∠AOC；
（2）根据对顶角的性质可求∠AOC，根据邻补角的概念可求∠AOC，再利用对顶角的性质可求∠BOD．
点评：本题考查了邻补角、对顶角，解题的关键是理解邻补角、对顶角的概念，并会运用其性质．