
【题目】如图,我市某中学在创建“特色校园”的活动中,将学校的办学理念做成了宣传牌(CD),放置在教学楼的顶部(如图所示),该中学数学活动小组的同学在山坡坡脚A处测得宣传牌底D的仰角为60°,沿坡AB向上走到B处测得宣传牌顶部C的仰角为45°.已知山坡AB的坡度为![]() ,AB=10米,AE=15米.
,AB=10米,AE=15米.
(1)求点B距水平面AE的高度BH;
(2)求宣传牌CD的高度.(结果精确到0.1米.参考数据:![]() ,
,![]() )
)
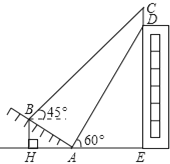
【答案】(1)BH=5 (2)2.7
【解析】分析:(1)在Rt△ABH中,由tan∠BAH=![]() .得到∠BAH=30°,于是得到结果BH=AB.sin∠BAH=10.sin30°=10×
.得到∠BAH=30°,于是得到结果BH=AB.sin∠BAH=10.sin30°=10×![]() =5;
=5;
(2)在Rt△ABH中,AH=AB.cos∠BAH=10.cos30°=5![]() ,在Rt△ADE中,tan∠DAE=
,在Rt△ADE中,tan∠DAE=![]() ,即tan60°=
,即tan60°=![]() ,得到DE=15
,得到DE=15![]() ,如图,过点B作BF⊥CE,垂足为F,求出BF=AH+AE=5
,如图,过点B作BF⊥CE,垂足为F,求出BF=AH+AE=5![]() +15,于是得到DF=DE-EF=DE-BH=15
+15,于是得到DF=DE-EF=DE-BH=15![]() -5,在Rt△BCF中,∠C=90°-∠CBF=90°-45°=45°,求得∠C=∠CBF=45°,得出CF=BF=5
-5,在Rt△BCF中,∠C=90°-∠CBF=90°-45°=45°,求得∠C=∠CBF=45°,得出CF=BF=5![]() +15,即可求得结果.
+15,即可求得结果.
详解:(1)在Rt△ABH中,
∵tan∠BAH=![]() .
.
∴∠BAH=30°,
∴BH=AB.sin∠BAH=10.sin30°=10×![]() =5.
=5.
答:点B距水平面AE的高度BH是5米;
(2)在Rt△ABH中,AH=AB.cos∠BAH=10.cos30°=5![]() ,
,
在Rt△ADE中,tan∠DAE=![]() ,
,
即tan60°=![]() ,∴DE=15
,∴DE=15![]() ,
,
如图,过点B作BF⊥CE,垂足为F,
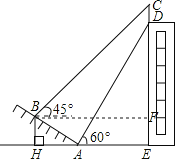
∴BF=AH+AE=5![]() +15,
+15,
DF=DE-EF=DE-BH=15![]() -5,
-5,
在Rt△BCF中,∠C=90°-∠CBF=90°-45°=45°,
∴∠C=∠CBF=45°,
∴CF=BF=5![]() +15,
+15,
∴CD=CF-DF=5![]() +15-(15
+15-(15![]() -5)=20-10
-5)=20-10![]() ≈20-10×1.732≈2.7(米),
≈20-10×1.732≈2.7(米),
答:广告牌CD的高度约为2.7米.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】松雷中学图书馆近日购进甲、乙两种图书,每本甲图书的进价比每本乙图书的进价高20元,花780元购进甲图书的数量与花540元购进乙图书的数量相同.
(1)求甲、乙两种图书每本的进价分别是多少元?
(2)松雷中学计划购进甲、乙两种图书共70本,总购书费用不超过4000元,则最多购进甲种图书多少本?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算:
(1)5![]() -3
-3![]() +4
+4![]() -
-![]()
(2)(![]() -
-![]() -
-![]() )×(-36)
)×(-36)
(3)-![]() ―(1―0.5)÷
―(1―0.5)÷![]() ×[2+(-4)2]
×[2+(-4)2]
(4)(![]() -
-![]() )×52÷|-
)×52÷|-![]() |+(
|+(![]() )2019×42020
)2019×42020
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】点![]() (
(![]() ,0)是
,0)是![]() 轴上的一个动点,它与原点的距离的2倍为
轴上的一个动点,它与原点的距离的2倍为![]() .
.
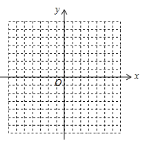
(1)求![]() 关于
关于![]() 的函数解析式,并在所给网格中画出这个函数图象;
的函数解析式,并在所给网格中画出这个函数图象;
(2)若反比例函数![]() =
=![]() 的图象与函数
的图象与函数![]() 的图象相交于点
的图象相交于点![]() ,且点
,且点![]() 的纵坐标为2.
的纵坐标为2.
①求k的值;
②结合图象,当![]() >
>![]() 时,写出
时,写出![]() 的取值范围.
的取值范围.
(3)过原点的一条直线交![]() =
=![]() (
(![]() >0)于
>0)于![]() 、
、![]() 两点(点
两点(点![]() 在点
在点![]() 的右侧),分别过点
的右侧),分别过点![]() 、
、![]() 作
作![]() 轴和
轴和![]() 轴的平行线,两平行线交于点
轴的平行线,两平行线交于点![]() ,则△
,则△![]() 的面积是 .
的面积是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
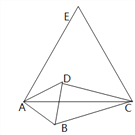
【题目】如图,四边形ABCD中,AD//BC,AD=AB=2,∠B=120°,∠ADC=150°,现以对角线AC为边向点D一侧作等边△ACE,则四边形ABCE的面积=______.
查看答案和解析>>
科目:初中数学 来源: 题型:
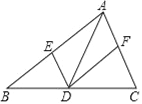
【题目】在△ABC中,点D是边BC上的点(与B,C两点不重合),过点D作DE∥AC,DF∥AB,分别交AB,AC于E,F两点,下列说法正确的是( )
A. 若AD⊥BC,则四边形AEDF是矩形
B. 若AD垂直平分BC,则四边形AEDF是矩形
C. 若BD=CD,则四边形AEDF是菱形
D. 若AD平分∠BAC,则四边形AEDF是菱形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数轴上A、B、C三点分别对应实数a、1、c,且BC-AB=AC.下列选项中,满足A、B、C三点在数轴上的位置关系是( )
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】巴南区认真落实“精准扶贫”.某“建卡贫困户”在党和政府的关怀和帮助下投资了一个鱼塘,经过一年多的精心养殖,今年10月份从鱼塘里捕捞了草鱼和花鲢共2500千克,在市场上草鱼以每千克16元的价格出售,花鲢以每千克24元的价格出售,这样该贫困户10月份收入52000元,
(1)今年10月份从鱼塘里捕捞草鱼和花鲢各多少千克?
(2)该贫困户今年12月份再次从鱼塘里捕捞.捕捞数量和销售价格上,草鱼数量比10月份减少了![]() 千克,销售价格不变;花鲢数量比10月份减少了
千克,销售价格不变;花鲢数量比10月份减少了![]() ,销售价格比10月份减少了
,销售价格比10月份减少了![]() ,该贫困户在10月份和12月份两次捕捞中共收入了94040元,真正达到了脱贫致富,求
,该贫困户在10月份和12月份两次捕捞中共收入了94040元,真正达到了脱贫致富,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com