
分析 ①先提取公因式,再进一步利用平方差公式因式分解计算即可;
②根据单项式与单项式相乘,把他们的系数分别相乘,相同字母的幂分别相加,其余字母连同他的指数不变,作为积的因式,计算即可;
③方程组利用加减消元法求出解即可;
④先解不等式组中每一个不等式的解集,再利用求不等式组解集的口诀“小小取小”即可确定结果;
⑤先根据乘法公式算乘法,再合并同类项,最后代入求出即可.
解答 解:①3.14×5.52-3.14×4.52
=3.14(5.52-4.52)
3.14(5.5+4.5)(5.5-4.5)
=3.14×10×1
=31.4;
②(-3x2y)•(-$\frac{1}{3}$xy2)÷xy3
=[(-3)(-$\frac{1}{3}$)]•(x2•x)(y•y2)÷xy3
=x3y3÷xy3
=x2;
③$\left\{\begin{array}{l}{3x+4y=19①}\\{x-y=4②}\end{array}\right.$
①+②×4得
7x=35,
x=5,
把x=5代入②得
5-y=4,
y=1,
∴原方程组的解为
$\left\{\begin{array}{l}{x=5}\\{y=1}\end{array}\right.$;
④$\left\{\begin{array}{l}{x-3(x-2)≥4①}\\{\frac{1+2x}{3}>x-1②}\end{array}\right.$
解不等式①得
x≤1,
解不等式②得
x<4,
∴不等式组的解为x≤1;
⑤(a+b)(a-b)+(a+b)2
=a2-b2+a2+2ab+b2
=2a2+2ab
当a=-1,b=$\frac{1}{2}$
原式=2×(-1)2+2×(-1)×$\frac{1}{2}$
=2-1
=1.
点评 本题主要考查了因式分解,单项式乘法,二元一次方程组,不等式组,多项式乘法,合并同类项,熟记这些法则和熟练掌握这些方法是解题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 在如图所示的正方形网格中,每个小正方形的边长均为1,△ABC的顶点A、C的坐标分别为(-4,5),(-1,3).
在如图所示的正方形网格中,每个小正方形的边长均为1,△ABC的顶点A、C的坐标分别为(-4,5),(-1,3).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
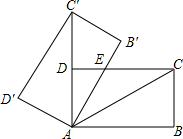 如图,将矩形ABCD绕点A旋转至矩形A′B′C′D′的位置,此时AC的中点恰好与D点重合,AB′交CD于点E.若AB=3,则△AEC的面积为( )
如图,将矩形ABCD绕点A旋转至矩形A′B′C′D′的位置,此时AC的中点恰好与D点重合,AB′交CD于点E.若AB=3,则△AEC的面积为( )| A. | 3 | B. | 1.5 | C. | $2\sqrt{3}$ | D. | $\sqrt{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com