
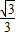 x-
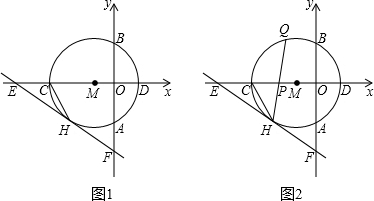
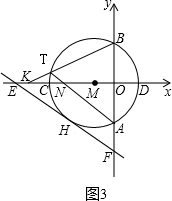
x-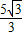 与⊙M相切于点H,交x轴于点E,交y轴于点F.
与⊙M相切于点H,交x轴于点E,交y轴于点F.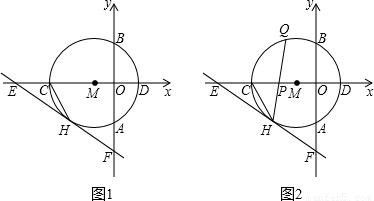
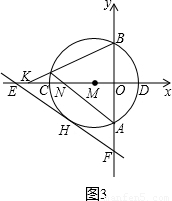
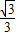 x-
x-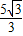 中,令y=0,可求得E的坐标,即可得到OE的长为5;连接MH,根据△EMH与△EFO相似即可求得半径为2;再由EC=MC=2,∠EHM=90°,可知CH是RT△EHM斜边上的中线,根据直角三角形斜边上的中线等于斜边的一半即可得出CH的长;
中,令y=0,可求得E的坐标,即可得到OE的长为5;连接MH,根据△EMH与△EFO相似即可求得半径为2;再由EC=MC=2,∠EHM=90°,可知CH是RT△EHM斜边上的中线,根据直角三角形斜边上的中线等于斜边的一半即可得出CH的长;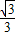 x-
x-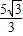 中,令y=0,则x=-5,即OE=5;
中,令y=0,则x=-5,即OE=5; ,故F点坐标为(0,-
,故F点坐标为(0,-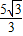 ),
),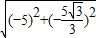 =
=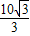 ,
,
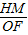 =
= ,即
,即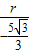 =
=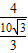 ,
, EM=2.
EM=2. .
.
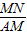 =
=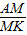 ;
;

科目:初中数学 来源: 题型:
| ||
| 3 |
5
| ||
| 3 |
查看答案和解析>>
科目:初中数学 来源:第3章《圆》中考题集(17):3.1 圆(解析版) 题型:解答题
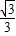 x-
x-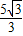 与⊙M相切于点H,交x轴于点E,交y轴于点F.
与⊙M相切于点H,交x轴于点E,交y轴于点F.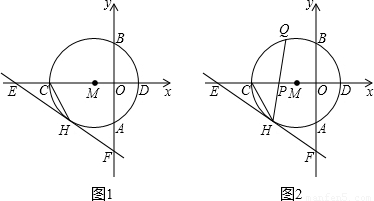
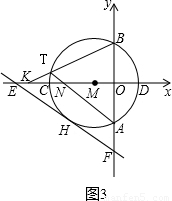
查看答案和解析>>
科目:初中数学 来源:第1章《解直角三角形》中考题集(11):1.1 锐角三角函数(解析版) 题型:解答题
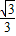 x-
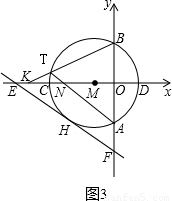
x-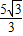 与⊙M相切于点H,交x轴于点E,交y轴于点F.
与⊙M相切于点H,交x轴于点E,交y轴于点F.
查看答案和解析>>
科目:初中数学 来源:第31章《锐角三角函数》中考题集(04):31.1 锐角三角函数(解析版) 题型:解答题
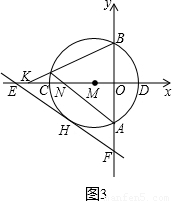
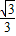 x-
x-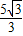 与⊙M相切于点H,交x轴于点E,交y轴于点F.
与⊙M相切于点H,交x轴于点E,交y轴于点F.
查看答案和解析>>
科目:初中数学 来源:2010年全国中考数学试题汇编《图形的相似》(03)(解析版) 题型:解答题
 x-
x-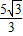 与⊙M相切于点H,交x轴于点E,交y轴于点F.
与⊙M相切于点H,交x轴于点E,交y轴于点F.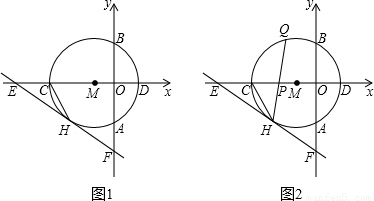

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com