
ЎҫМвДҝЎҝИзНјЈ¬ФЪRtЎчABCЦРЈ¬ЎПACBЈҪ90ЎгЈ¬ACЈҪ16Ј¬BCЈҪ12Ј¬өгDЎўE·ЦұрОӘұЯABЎўBCЦРөгЈ¬өгPҙУөгAіц·ўЈ¬СШЙдПЯAB·ҪПтТФГҝГл5ёцөҘО»іӨ¶ИөДЛЩ¶ИПтөгBФЛ¶ҜЈ¬өҪөгBНЈЦ№Ј®өұөгPІ»УлөгAЦШәПКұЈ¬№эөгPЧчPQЎОACЈ¬ЗТөгQФЪЦұПЯABЧуІаЈ¬APЈҪPQЈ¬№эөгQЧчQMЎНABҪ»ЙдПЯABУЪөгMЈ®ЙиөгPФЛ¶ҜөДКұјдОӘtЈЁГлЈ©
ЈЁ1Ј©УГә¬tөДҙъКэКҪұнКҫПЯ¶ОDMөДіӨ¶ИЈ»
ЈЁ2Ј©ЗуөұөгQВдФЪBCұЯЙПКұtөДЦөЈ»
ЈЁ3Ј©ЙиЎчPQMУлЎчDEBЦШөюІҝ·ЦНјРОөДГж»эОӘSЈЁЖҪ·ҪөҘО»Ј©Ј¬өұЎчPQMУлЎчDEBУРЦШөюЗТЦШөюІҝ·ЦНјРОКЗИэҪЗРОКұЈ¬ЗуSУлtөДәҜКэ№ШПөКҪЈ»
ЈЁ4Ј©өұҫӯ№эөгCәНЎчPQMЦРТ»ёц¶ҘөгөДЦұПЯЖҪ·ЦЎчPQMөДДЪҪЗКұЈ¬ЦұҪУРҙіцҙЛКұtөДЦөЈ®

Ўҫҙр°ёЎҝЈЁ1Ј©өұ0ЈјtЎЬ![]() КұЈ¬DMЈҪ©Ғ9t+10Ј¬өұ
КұЈ¬DMЈҪ©Ғ9t+10Ј¬өұ![]() ЈјtЎЬ4КұЈ¬DMЈҪ9t©Ғ10Ј»ЈЁ2Ј©
ЈјtЎЬ4КұЈ¬DMЈҪ9t©Ғ10Ј»ЈЁ2Ј©![]() sЈ»ЈЁ3Ј©өұ
sЈ»ЈЁ3Ј©өұ![]() ЈјtЎЬ
ЈјtЎЬ![]() КұЈ¬ЦШөюІҝ·ЦКЗЎчDMKЈ¬SЈ©ЈҪ
КұЈ¬ЦШөюІҝ·ЦКЗЎчDMKЈ¬SЈ©ЈҪ![]() t2©Ғ
t2©Ғ![]() t+
t+![]() Ј®өұ
Ј®өұ![]() ЎЬtЎЬ4КұЈ¬ SЈҪ6t2©Ғ48t+96Ј®ЈЁ4Ј©tөДЦөОӘ
ЎЬtЎЬ4КұЈ¬ SЈҪ6t2©Ғ48t+96Ј®ЈЁ4Ј©tөДЦөОӘ![]() s»т
s»т![]() sЈ®
sЈ®
ЎҫҪвОцЎҝ
ЈЁ1Ј©·ЦөгMФЪПЯ¶ОADЙП»төгMФЪПЯ¶ОADөДСУіӨПЯКұБҪЦЦЗйРО·ЦұрЗуҪвЈ®
ЈЁ2Ј©өұөгQВдФЪBCЙПКұЈ¬УЙPQЎОACЈ¬ҝЙөГ![]() Ј¬УЙҙЛ№№ҪЁ·ҪіМјҙҝЙҪвҫцОКМвЈ®
Ј¬УЙҙЛ№№ҪЁ·ҪіМјҙҝЙҪвҫцОКМвЈ®
ЈЁ3Ј©·ЦБҪЦЦЗйРОЈәўЩИзНј3-1ЦРЈ¬өұ![]() ЈјtЎЬ
ЈјtЎЬ![]() КұЈ¬ЦШөюІҝ·ЦКЗЎчDMKЈ®ўЪИзНј3-2ЦРЈ¬өұ
КұЈ¬ЦШөюІҝ·ЦКЗЎчDMKЈ®ўЪИзНј3-2ЦРЈ¬өұ![]() ЎЬtЎЬ4КұЈ¬ЦШөюІҝ·ЦКЗЎчPBKЈ¬·ЦұрЗуҪвЈ®ЈЁ4Ј©·ЦБҪЦЦЗйРОЈәўЩИзНј4-1ЦРЈ¬өұЦұПЯCQЖҪ·ЦЎПPQMКұЈ¬ЙиЦұПЯCQҪ»ABУЪGЈ¬ЧчGKЎНPQУЪKЈ®АыУГИ«өИИэҪЗРОөДРФЦКЈ¬ЖҪРРПЯ·ЦПЯ¶ОіЙұИАэ¶ЁАнЈ¬№№ҪЁ·ҪіМјҙҝЙЈ®ўЪИзНј4-2ЦРЈ¬өұCMЖҪ·ЦЎПQMPКұЈ¬ЧчCGЎНABУЪGЈ®ЗуіцAMөДіӨЈ¬№№ҪЁ·ҪіМјҙҝЙҪвҫцОКМвЈ®
ЎЬtЎЬ4КұЈ¬ЦШөюІҝ·ЦКЗЎчPBKЈ¬·ЦұрЗуҪвЈ®ЈЁ4Ј©·ЦБҪЦЦЗйРОЈәўЩИзНј4-1ЦРЈ¬өұЦұПЯCQЖҪ·ЦЎПPQMКұЈ¬ЙиЦұПЯCQҪ»ABУЪGЈ¬ЧчGKЎНPQУЪKЈ®АыУГИ«өИИэҪЗРОөДРФЦКЈ¬ЖҪРРПЯ·ЦПЯ¶ОіЙұИАэ¶ЁАнЈ¬№№ҪЁ·ҪіМјҙҝЙЈ®ўЪИзНј4-2ЦРЈ¬өұCMЖҪ·ЦЎПQMPКұЈ¬ЧчCGЎНABУЪGЈ®ЗуіцAMөДіӨЈ¬№№ҪЁ·ҪіМјҙҝЙҪвҫцОКМвЈ®
ҪвЈәЈЁ1Ј©ИзНј1ЦРЈ¬

ФЪRtABCЦРЈ¬ЎЯACЈҪ16Ј¬BCЈҪ12Ј¬ЎПCЈҪ90ЎгЈ¬
ЎаABЈҪ![]() Ј¬
Ј¬
ЎЯPQЎОACЈ¬
ЎаЎПAЈҪЎПQPMЈ¬
ЎЯЎПCЈҪЎПPMQЈҪ90ЎгЈ¬
ЎаЎчACBЎЧЎчPMQЈ¬
Ўа![]() ,
,
Ўа![]() ,
,
ЎаPMЈҪ4tЈ¬MQЈҪ3tЈ¬
өұ0ЈјtЎЬ![]() КұЈ¬DMЈҪAD©ҒAMЈҪ10©Ғ5t©Ғ4tЈҪ©Ғ9t+10Ј®
КұЈ¬DMЈҪAD©ҒAMЈҪ10©Ғ5t©Ғ4tЈҪ©Ғ9t+10Ј®
өұ![]() ЈјtЎЬ4КұЈ¬DMЈҪAM©ҒADЈҪ9t©Ғ10Ј®
ЈјtЎЬ4КұЈ¬DMЈҪAM©ҒADЈҪ9t©Ғ10Ј®
ЈЁ2Ј©ИзНј2ЦРЈ¬

өұөгQВдФЪBCЙПКұЈ¬ЎЯPQЎОACЈ¬
Ўа![]() ,
,
Ўа![]() Ј¬
Ј¬
ҪвөГtЈҪ![]() Ј¬
Ј¬
ЎаөұөгQВдФЪBCұЯЙПКұtөДЦөОӘ![]() sЈ®
sЈ®
ЈЁ3Ј©ИзНј3©Ғ1ЦРЈ¬өұ![]() ЈјtЎЬ
ЈјtЎЬ![]() КұЈ¬ЦШөюІҝ·ЦКЗЎчDMKЈ¬SЈҪ
КұЈ¬ЦШөюІҝ·ЦКЗЎчDMKЈ¬SЈҪ![]() ЎБDMЎБMKЈҪ
ЎБDMЎБMKЈҪ![]() ЎБЈЁ9t©Ғ10Ј©ЎБ
ЎБЈЁ9t©Ғ10Ј©ЎБ![]() ЈЁ9t©Ғ10Ј©ЈҪ
ЈЁ9t©Ғ10Ј©ЈҪ![]() t2©Ғ
t2©Ғ![]() t+
t+![]() Ј®
Ј®

ИзНј3©Ғ2ЦРЈ¬өұ![]() ЎЬtЎЬ4КұЈ¬ЦШөюІҝ·ЦКЗЎчPBKЈ¬SЈҪ
ЎЬtЎЬ4КұЈ¬ЦШөюІҝ·ЦКЗЎчPBKЈ¬SЈҪ![]() PKBKЈҪ
PKBKЈҪ![]() ЎБ
ЎБ![]() ЈЁ20©Ғ5span>tЈ©
ЈЁ20©Ғ5span>tЈ©![]() ЈЁ20©Ғ5tЈ©ЈҪ6t2©Ғ48t+96Ј®
ЈЁ20©Ғ5tЈ©ЈҪ6t2©Ғ48t+96Ј®

ЈЁ4Ј©ИзНј4©Ғ1ЦРЈ¬өұЦұПЯCQЖҪ·ЦЎПPQMКұЈ¬ЙиЦұПЯCQҪ»ABУЪGЈ¬ЧчGKЎНPQУЪKЈ®
ЎЯЎПQKGЈҪЎПQMGЈҪ90ЎгЈ¬ЎПGQKЈҪЎПGQMЈ¬QGЈҪQGЈ¬
ЎаЎчQGKЎХЎчQGMЈЁAASЈ©Ј¬
ЎаQKЈҪQMЈҪ3tЈ¬PKЈҪPQ©ҒQKЈҪ5t©Ғ3tЈҪ2tЈ¬
ЎаPGЈҪ![]() PKЈҪ
PKЈҪ![]() tЈ¬
tЈ¬
ЎЯPQЎОACЈ¬
Ўа![]() Ј¬
Ј¬
Ўа Ј¬
Ј¬
ЎаtЈҪ![]() Ј®
Ј®
ИзНј4©Ғ2ЦРЈ¬өұCMЖҪ·ЦЎПQMPКұЈ¬ЧчCGЎНABУЪGЈ®

ЎЯ![]() ACBCЈҪ
ACBCЈҪ![]() ABCGЈ¬
ABCGЈ¬
ЎаCGЈҪ![]() Ј¬AGЈҪ
Ј¬AGЈҪ Ј¬
Ј¬
ЎЯЎПCMGЈҪЎПGCMЈҪ45ЎгЈ¬
ЎаCGЈҪGMЈҪ![]() Ј¬
Ј¬
ЎаAMЈҪ9tЈҪ![]() Ј¬
Ј¬
ҪвөГtЈҪ![]() Ј¬
Ј¬
ЧЫЙПЛщКцЈ¬ВъЧгМхјюөДtөДЦөОӘ![]() s»т
s»т![]() sЈ®
sЈ®



| Дкј¶ | ёЯЦРҝОіМ | Дкј¶ | іхЦРҝОіМ |
| ёЯТ» | ёЯТ»Гв·СҝОіМНЖјцЈЎ | іхТ» | іхТ»Гв·СҝОіМНЖјцЈЎ |
| ёЯ¶ю | ёЯ¶юГв·СҝОіМНЖјцЈЎ | іх¶ю | іх¶юГв·СҝОіМНЖјцЈЎ |
| ёЯИэ | ёЯИэГв·СҝОіМНЖјцЈЎ | іхИэ | іхИэГв·СҝОіМНЖјцЈЎ |
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝИзНјЈ¬RtЎчABCЦҪЖ¬ЦРЈ¬ЎПC=90ЎгЈ¬AC=6Ј¬BC=8Ј¬өгDФЪұЯBC ЙПЈ¬ТФADОӘХЫәЫҪ«ЎчABDХЫөюөГөҪЎчABЎдD,ABЎдУлұЯBCҪ»УЪөгEЈ®ИфЎчDEBЎдОӘЦұҪЗИэҪЗРОЈ¬ФтBDөДіӨКЗ_______Ј®

Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝЛжЧЕОТКЎЎ°ҙуГАЗаәЈЈ¬ГААцПД¶јЎұУ°ПмБҰөДА©ҙуЈ¬ФҪАҙФҪ¶аөДУОҝНДҪГы¶шАҙЎЈёщҫЭЗаәЈКЎВГУОҫЦЎ¶2015Дк№ъЗміӨјЩіцУОЗчКЖұЁёжЎ·»жЦЖБЛИзПВЙРІ»НкХыөДНіјЖНјЎЈ
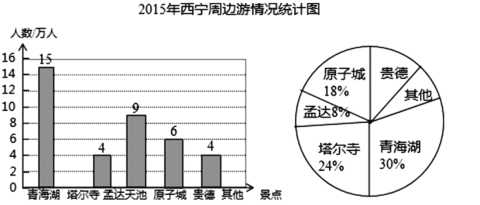
ёщҫЭТФЙПРЕПўҪвҙрПВБРОКМвЈә
(1)2015Дк№ъЗмЖЪјдЈ¬ОчДюЦЬұЯҫ°Зш№ІҪУҙэУОҝН___НтИЛЈ¬ЙИРОНіјЖНјЦРЎ°ЗаәЈәюЎұЛщ¶ФУҰөДФІРДҪЗөД¶ИКэКЗ___Ј¬ІўІ№И«МхРОНіјЖНјЈ»
(2)јЧТТБҪёцВГРРНЕФЪЗаәЈәюЎўЛю¶ыЛВЎўФӯЧУіЗИэёцҫ°өгЦРЈ¬Н¬КұСЎФсИҘН¬Т»ёцҫ°өгөДёЕВККЗ¶аЙЩ?ЗлУГ»ӯКчЧҙНј»тБРұн·ЁјУТФЛөГчЈ¬ІўБРҫЩЛщУРөИҝЙДЬөДҪб№ыЎЈ
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝҪв·ҪіМЈә
ЈЁ1Ј©x2©Ғ11x©Ғ12ЈҪ0ЈЁТтКҪ·ЦҪв·ЁЈ©
ЈЁ2Ј©x2+4x©Ғ5ЈҪ0ЈЁЕд·Ҫ·ЁЈ©
ЈЁ3Ј©ЈЁx+2Ј©2©Ғ10ЈЁx+2Ј©+25ЈҪ0ЈЁТтКҪ·ЦҪв·ЁЈ©
ЈЁ4Ј©2x2©Ғ7x+3ЈҪ0ЈЁ№«КҪ·ЁЈ©
ЈЁ5Ј©©Ғx2+4xЈҪ3ЈЁ·Ҫ·ЁЧФСЎЈ©
ЈЁ6Ј©ўЮЈЁx©Ғ2Ј©ЈЁ2x+1Ј©ЈҪ1+2xЈЁ·Ҫ·ЁЧФСЎЈ©
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
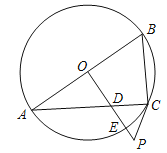
ЎҫМвДҝЎҝИзНјЈ¬ТСЦӘABКЗЎСOөДЦұҫ¶Ј¬№эOөгЧчOPЎНABЈ¬Ҫ»ПТACУЪөгDЈ¬Ҫ»ЎСOУЪөгEЈ¬ЗТК№ЎПPCA=ЎПABCЈ®
(1)ЗуЦӨЈәPCКЗЎСOөДЗРПЯЈ»
(2)ИфЎПP=60ЎгЈ¬PC=2Ј¬ЗуPEөДіӨЈ®
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝБјәГөДТыКі¶ФС§ЙъөДЙнМеЎўЦЗБҰ·ўУэәНҪЎҝөЖрөҪБЛј«ЖдЦШТӘөДЧчУГЈ¬»зІЛЦРө°°ЧЦКЎўёЖЎўБЧј°Ц¬ИЬРФО¬ЙъЛШУЕУЪЛШКіЈ¬¶шЛШКіЦРІ»ұҘәНЦ¬·ҫЛбЎўО¬ЙъЛШәНПЛО¬ЛШУЦУЕУЪ»зКіЈ¬Ц»УР»зКіУлЛШКіККөұҙоЕдЈ¬ІЕДЬЗҝ»ҜіхЦРЙъөДЙнМеЛШЦКЈ®ДіРЈОӘБЛБЛҪвС§ЙъөДМеЦКҪЎҝөЧҙҝцЈ¬ТФұгКіМГОӘС§ЙъМṩәПАнЙЕКіЈ¬¶ФұҫРЈЖЯДкј¶Ўў°ЛДкј¶С§ЙъөДМеЦКҪЎҝөЧҙҝцҪшРРБЛөчІйЈ¬№эіМИзПВЈә
КХјҜКэҫЭЈәҙУЖЯЎў°ЛДкј¶БҪёцДкј¶ЦРёчійИЎ15ГыС§ЙъЈ¬ҪшРРБЛМеЦКҪЎҝөІвКФЈ¬ІвКФіЙјЁЈЁ°Щ·ЦЦЖЈ©ИзПВЈә
ЖЯДкј¶Јә74 81 75 76 70 75 75 79 81 70 74 80 91 69 82
°ЛДкј¶Јә81 94 83 77 83 80 81 70 81 73 78 82 80 70 50
ХыАнКэҫЭЈә
Дкј¶ | xЈј60 | 60ЎЬxЈј80 | 80ЎЬxЈј90 | 90ЎЬxЎЬ100 |
ЖЯДкј¶ | 0 | 10 | 4 | 1 |
°ЛДкј¶ | 1 | 5 | 8 | 1 |
ЈЁЛөГчЈә90·Цј°ТФЙПОӘУЕРгЈ¬80Ў«90·ЦЈЁІ»ә¬90·ЦЈ©ОӘБјәГЈ¬60Ў«80·ЦЈЁІ»ә¬80·ЦЈ©ОӘј°ёсЈ¬60·ЦТФПВОӘІ»ј°ёсЈ©
·ЦОцКэҫЭЈә
Дкј¶ | ЖҪҫщКэ | ЦРО»Кэ | ЦЪКэ |
ЖЯДкј¶ | ЎЎ ЎЎ | 75 | 75 |
°ЛДкј¶ | 77.5 | 80 | ЎЎ ЎЎ |
өГіцҪбВЫЈә
ЈЁ2Ј©ҝЙТФНЖ¶ПіцЎЎ ЎЎДкј¶С§ЙъөДМеЦКҪЎҝөЧҙҝцёьәГТ»Р©Ј¬ІўЛөГчАнУЙЈ»
ЈЁ3Ј©ИфЖЯДкј¶№ІУР300ГыС§ЙъЈ¬Зл№АјЖЖЯДкј¶МеЦКҪЎҝөіЙјЁУЕРгөДС§ЙъИЛКэЈ®
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝРЎАоФЪҫ°ЗшПъКЫТ»ЦЦВГУОјНДоЖ·Ј¬ТСЦӘГҝјюҪшјЫОӘ6ФӘЈ¬өұПъКЫөҘјЫ¶ЁОӘ8ФӘКұЈ¬ГҝМмҝЙТФПъКЫ200јюЈ®КРіЎөчІй·ҙУіЈәПъКЫөҘјЫГҝМбёЯ1ФӘЈ¬ИХПъБҝҪ«»бјхЙЩ10јюЈ¬ОпјЫІҝГЕ№ж¶ЁЈәПъКЫөҘјЫІ»ДЬі¬№э12ФӘЈ¬ЙиёГјНДоЖ·өДПъКЫөҘјЫОӘxЈЁФӘЈ©Ј¬ИХПъБҝОӘyЈЁјюЈ©Ј¬ИХПъКЫАыИуОӘwЈЁФӘЈ©Ј®
ЈЁ1Ј©ЗуyУлxөДәҜКэ№ШПөКҪЈ®
ЈЁ2Ј©ТӘК№ИХПъКЫАыИуОӘ720ФӘЈ¬ПъКЫөҘјЫУҰ¶ЁОӘ¶аЙЩФӘЈҝ
ЈЁ3Ј©ЗуИХПъКЫАыИуwЈЁФӘЈ©УлПъКЫөҘјЫxЈЁФӘЈ©өДәҜКэ№ШПөКҪЈ¬өұxОӘәОЦөКұЈ¬ИХПъКЫАыИуЧоҙуЈ¬ІўЗуіцЧоҙуАыИуЈ®
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
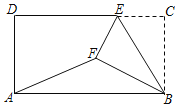
ЎҫМвДҝЎҝИзНјЈ¬ФЪҫШРОABCDЦРЈ¬ABЈҪ4Ј¬BCЈҪ![]() Ј¬EОӘCDұЯЙПТ»өгЈ¬Ҫ«ЎчBCEСШBEХЫөюЈ¬К№өГCВдөҪҫШРОДЪөгFөДО»ЦГЈ¬Б¬ҪУAFЈ¬ИфtanЎПBAFЈҪ
Ј¬EОӘCDұЯЙПТ»өгЈ¬Ҫ«ЎчBCEСШBEХЫөюЈ¬К№өГCВдөҪҫШРОДЪөгFөДО»ЦГЈ¬Б¬ҪУAFЈ¬ИфtanЎПBAFЈҪ![]() Ј¬ФтCEЈҪ_____Ј®
Ј¬ФтCEЈҪ_____Ј®
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝҫШРОЦҪЖ¬![]() Ј¬
Ј¬![]() Ј¬
Ј¬![]() Ј¬ФЪҫШРОұЯЙПУРТ»өгPЈ¬ЗТ
Ј¬ФЪҫШРОұЯЙПУРТ»өгPЈ¬ЗТ![]() Ј¬Ҫ«ҫШРОЦҪЖ¬ХЫөюЈ¬К№өгCУлөгPЦШәПЈ¬ХЫәЫЛщФЪЦұПЯҪ»ҫШРОБҪұЯУЪөгEЈ¬FЈ¬ФтEFіӨОӘ_______.
Ј¬Ҫ«ҫШРОЦҪЖ¬ХЫөюЈ¬К№өгCУлөгPЦШәПЈ¬ХЫәЫЛщФЪЦұПЯҪ»ҫШРОБҪұЯУЪөгEЈ¬FЈ¬ФтEFіӨОӘ_______.
Ійҝҙҙр°ёәНҪвОц>>
°Щ¶ИЦВРЕ - Б·П°ІбБРұн - КФМвБРұн
әюұұКЎ»ҘБӘНшОҘ·ЁәНІ»БјРЕПўҫЩұЁЖҪМЁ | НшЙПУРәҰРЕПўҫЩұЁЧЁЗш | өзРЕХ©ЖӯҫЩұЁЧЁЗш | ЙжАъК·РйОЮЦчТеУРәҰРЕПўҫЩұЁЧЁЗш | ЙжЖуЗЦИЁҫЩұЁЧЁЗш
ОҘ·ЁәНІ»БјРЕПўҫЩұЁөз»°Јә027-86699610 ҫЩұЁУКПдЈә58377363@163.com