
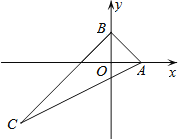
【题目】如图,△ABC在平面直角坐标系中,点A、B分别在x轴和y轴上,且OA=OB,边AC所在直线解析式为y=![]() x﹣
x﹣![]() ,若△ABC的内心在y轴上,则tan∠ACB的值为( )
,若△ABC的内心在y轴上,则tan∠ACB的值为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】B
【解析】
△ABO是等腰直角三角形,然后根据△ABC的内心在y轴上,则BO是∠ABC的平分线,△ABC是直角三角形,求得BC的解析式,进而求得BC的长,然后根据三角函数的定义求解.
在y=![]() x﹣
x﹣![]() 中,令y=0,则
中,令y=0,则![]() x﹣
x﹣![]() =0,解得x=1,
=0,解得x=1,
∵OA=OB,
∴B的坐标是(0,1),AB=![]() ,△OAB是等腰直角三角形.
,△OAB是等腰直角三角形.
∴∠ABO=45°
∵△ABC的内心在y轴上,
∴∠ABC=2∠ABO=90°,即△ABC是直角三角形,
设BC的解析式是y=x+c,
则把B(0,1)代入得c=1,
则BC的解析式是y=x+1,
根据题意得: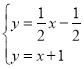 ,
,
解得:![]() ,
,
即C的坐标是(﹣3,﹣2).
∵B(0,1)
则BC=![]() ,
,
则![]() .
.
故选:B.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,抛物线
,抛物线![]() 经过点
经过点![]() ,
,![]() .
.

(1)求点B的坐标和抛物线的解析式;
(2)M(m,0)为x轴上一个动点,过点M垂直于x轴的直线与直线AB和抛物线分别交于点P、N,
①点![]() 在线段
在线段![]() 上运动,若以
上运动,若以![]() ,
,![]() ,
,![]() 为顶点的三角形与
为顶点的三角形与![]() 相似,求点
相似,求点![]() 的坐标;
的坐标;
②点![]() 在
在![]() 轴上自由运动,若三个点
轴上自由运动,若三个点![]() ,
,![]() ,
,![]() 中恰有一点是其它两点所连线段的中点(三点重合除外),则称
中恰有一点是其它两点所连线段的中点(三点重合除外),则称![]() ,
,![]() ,
,![]() 三点为“共谐点”.请直接写出使得
三点为“共谐点”.请直接写出使得![]() ,
,![]() ,
,![]() 三点成为“共谐点”的
三点成为“共谐点”的![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某店在开学初用880元购进若干个学生专用科学计算器,按每个50元出售,很快就销售一空,据了解学生还急需3倍这种计算器,于是又用2580元购进所需计算器,由于量大每个进价比上次优惠1元,该店仍按每个50元销售,最后剩下4个按九折卖出.这笔生意该店共盈利( )元.
A.508 B.520 C.528 D.560
查看答案和解析>>
科目:初中数学 来源: 题型:
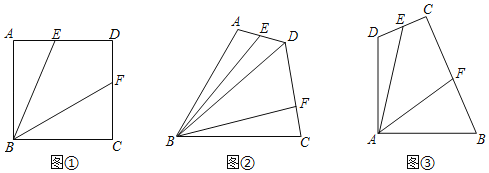
【题目】提出问题:(1)如图①,正方形ABCD中,点E,点F分别在边AD和边CD上,若正方形边长为4,DE+DF=4,则四边形BEDF的面积为 .
探究问题:(2)如图②,四边形ABCD,AB=BC=4,∠ABC=60°,∠ADC=120°,点E、F分别是边AD和边DC上的点,连接BE,BF,若ED+DF=3,BD=2![]() ,求四边形EBFD的面积;
,求四边形EBFD的面积;
解决问题:(3)某地质勘探队为了进行资源助测,建立了如图③所示的一个四边形野外勘查基地,基地相邻两侧边界DA、AB长度均为4km,∠DAB=90°,由于勘测需要及技术原因,主勘测仪C与基地边缘D、B夹角为90°(∠DCB=90°),在边界CD和边界BC上分别有两个辅助勘测仪E和F,辅助勘测仪E和F与主勘测仪C的距离之和始终等于4km(CE+CF=4).为了达到更好监测效果,需保证勘测区域(四边形EAFC)面积尽可能大.请问勘测区域面积有没有最大值,如果有求出最大值,如果没有,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知y=|y1|+y2﹣1,其中y1=x﹣3,y2与x成反比例关系,且当x=2时,y2=3.
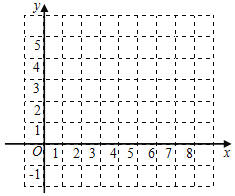
(1)根据给定的条件写出y与x的函数表达式及自变量x的取值范围: .
(2)当x>0时,根据y与x的函数表达式,选取适当的自变量x的值,完成下表,并根据表中数据,在平面直角坐标系xOy中描点,画出该函数x>0时的图象.
x | …… | …… | |||||||
y | …… | …… |
(3)当x>0时,结合函数图象,解决相关问题:估计y=﹣![]() x+5时,x的值约为 .(保留一位小数)
x+5时,x的值约为 .(保留一位小数)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AD∥BC,∠B=90°,AB=8,tan∠CAD=![]() ,CA=CD,E、F分别是AD、AC上的动点(点E与A、D不重合),且∠FEC=∠ACB.
,CA=CD,E、F分别是AD、AC上的动点(点E与A、D不重合),且∠FEC=∠ACB.
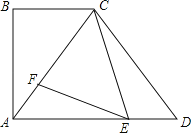
(1)求CD的长;
(2)若AF=2,求DE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】盒中有若干枚黑棋和白棋,这些棋除颜色外无其他差别,现让学生进行摸棋试验:每次摸出一枚棋,记录颜色后放回摇匀.重复进行这样的试验得到以下数据:
摸棋的次数n | 100 | 200 | 300 | 500 | 800 | 1000 |
摸到黑棋的次数m | 24 | 51 | 76 | 124 | 201 | 250 |
摸到黑棋的频率 | 0.240 | 0.255 | 0.253 | 0.248 | 0.251 | 0.250 |
(1)根据表中数据估计从盒中摸出一枚棋是黑棋的概率是 ;(精确到0.01)
(2)若盒中黑棋与白棋共有4枚,某同学一次摸出两枚棋,请计算这两枚棋颜色不同的概率,并说明理由
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AC为正方形ABCD的对角线,点E为DC边上一点(不与C、D重合),连接BE,以E为旋转中心,将线段EB逆时针旋转90°,得到线段EF,连接DF.
(1)请在图中补全图形.
(2)求证:AC∥DF.
(3)探索线段ED、DF、AC的数量关系,并加以证明.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com