
【题目】等腰三角形的一个角比另一个角的![]() 倍少
倍少![]() 度,则等腰三角形顶角的度数是( )
度,则等腰三角形顶角的度数是( )
A.![]() B.
B.![]() 或
或![]() C.
C.![]() 或
或![]() D.
D.![]() 或
或![]() 或
或![]()
【答案】D
【解析】
设另一个角是x,表示出一个角是2x-20°,然后分①x是顶角,2x-20°是底角,②x是底角,2x-20°是顶角,③x与2x-20°都是底角根据三角形的内角和等于180°与等腰三角形两底角相等列出方程求解即可.
设另一个角是x,表示出一个角是2x-20°,
①x是顶角,2x-20°是底角时,x+2(2x-20°)=180°,
解得x=44°,
∴顶角是44°;
②x是底角,2x-20°是顶角时,2x+(2x-20°)=180°,
解得x=50°,
∴顶角是2×50°-20°=80°;
③x与2x-20°都是底角时,x=2x-20°,
解得x=20°,
∴顶角是180°-20°×2=140°;
综上所述,这个等腰三角形的顶角度数是44°或80°或140°.
故答案为:D.


 快乐5加2金卷系列答案
快乐5加2金卷系列答案科目:初中数学 来源: 题型:
【题目】某校积极推进“阳光体育”工程,本学期在九年级11个班中开展篮球单循环比赛(每个班与其它班分别进行一场比赛,每班需进行10场比赛).比赛规则规定:每场比赛都要分出胜负,胜一场得3分,负一场得﹣1分.
(1)如果某班在所有的比赛中只得14分,那么该班胜负场数分别是多少?
(2)假设比赛结束后,甲班得分是乙班的3倍,甲班获胜的场数不超过5场,且甲班获胜的场数多于乙班,请你求出甲班、乙班各胜了几场.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,△ABC中,AD为BC边上的中线,则有S△ABD=S△ACD,许多面积问题可以转化为这个基本模型解答.如图②,已知△ABC的面积为1,把△ABC各边均顺次延长一倍,连结所得端点,得到△A1B1C1,即将△ABC向外扩展了一次,则扩展一次后的△A1B1C1的面积是_____,如图③,将△ABC向外扩展了两次得到△A2B2C2,……,若将△ABC向外扩展了n次得到△AnBnn,则扩展n次后得到的△AnBnn面积是_____.
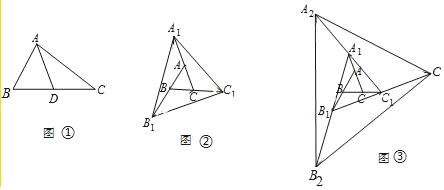
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知A ,D,B,E在同一条直线上,且AD = BE, AC = DF,补充下列其中一个条件后,不一定能得到△ABC≌△DEF 的是( )

A.BC = EFB.AC//DFC.∠C = ∠FD.∠BAC = ∠EDF
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】边长为a的等边三角形,记为第1个等边三角形,取其各边的三等分点,顺次连接得到一个正六边形,记为第1个正六边形,取这个正六边形不相邻的三边中点,顺次连接又得到一个等边三角形,记为第2个等边三角形,取其各边的三等分点,顺次连接又得到一个正六边形,记为第2个正六边形(如图),…,按此方式依次操作,则第6个正六边形的边长为( )
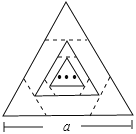
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某县为落实“精准扶贫惠民政策”,计划将某村的居民自来水管道进行改造.该工程若由甲队单独施工恰好在规定时间内完成;若乙队单独施工,则完成工程所需天数是规定天数的1.5倍.如果由甲、乙队先合作施工15天,那么余下的工程由甲队单独完成还需5天.
(1)这项工程的规定时间是多少天?
(2)为了缩短工期以减少对居民用水的影响,工程指挥部最终决定该工程由甲、乙两队合作完成.则甲、乙两队合作完成该工程需要多少天?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场销售一批名牌衬衫,平均每天可售出20件,每件赢利40元,为了扩大销售,增加利润,尽量减少库存,商场决定采取适当的降价措施.经调查发现,如果每件衬衫每降价2元,商场平均每天可多售出5件.求:
(1)若商场平均每天要赢利1400元,每件衬衫应降价多少元?
(2)每件衬衫降价多少元时,商场平均每天赢利最多?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com