
 如图,△ABC内接于⊙O,弦AD⊥AB交BC于点E,过点B作⊙O的切线交DA的延长线于点F,且∠ABF=∠ABC.
如图,△ABC内接于⊙O,弦AD⊥AB交BC于点E,过点B作⊙O的切线交DA的延长线于点F,且∠ABF=∠ABC.分析 (1)连结BD,如图,由AD⊥AB,根据圆周角定理的推理可得BD为⊙O的直径,再根据切线的性质得∠DBA+∠ABF=90°,则利用等角的余角相等得∠D=∠ABF,根据圆周角定理有∠D=∠C,已知条件有∠ABF=∠ABC.所以∠C=∠ABC,于是根据等腰三角形的判定定理即可得到AB=AC;
(2)利用∠D=∠ABF可得cosD=cos∠ABF=$\frac{4}{5}$,在Rt△ABD中利用三角函数得定义可计算出BD=5,利用勾股定理可计算出AB=3,接着证明Rt△ABE∽Rt△ADB,利用相似比可计算出AE=$\frac{9}{4}$,BE=$\frac{15}{4}$,则DE=AD-AE=4-$\frac{9}{4}$=$\frac{7}{4}$,然后证明△EDB∽△ECA,则可利用相似比计算出CE.
解答 (1)证明:连结BD,如图,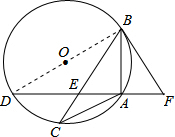 ∵AD⊥AB,
∵AD⊥AB,
∴∠BAD=90°,
∴BD为⊙O的直径,
∵BF为⊙O的切线,
∴BD⊥BF,
∴∠DBA+∠ABF=90°,
∵∠DBA+∠D=90°,
∴∠D=∠ABF,
∵∠D=∠C,∠ABF=∠ABC.
∴∠C=∠ABC,
∴AB=AC;
(2)解:∵∠D=∠ABF,
∴cosD=cos∠ABF=$\frac{4}{5}$,
在Rt△ABD中,∵cosD=$\frac{AD}{BD}$=$\frac{4}{5}$,
而AD=4,
∴BD=5,
∴AB=$\sqrt{{5}^{2}-{4}^{2}}$=3,
∵∠ABC=∠D,
∴Rt△ABE∽Rt△ADB,
∴$\frac{AE}{AB}$=$\frac{AB}{AD}$=$\frac{BE}{BD}$,即$\frac{AE}{3}$=$\frac{3}{4}$=$\frac{BE}{5}$,
∴AE=$\frac{9}{4}$,BE=$\frac{15}{4}$,
∴DE=AD-AE=4-$\frac{9}{4}$=$\frac{7}{4}$,
∵∠C=∠D,∠DBE=∠CAE,
∴△EDB∽△ECA,
∴$\frac{DE}{CE}$=$\frac{BE}{AE}$,即$\frac{\frac{7}{4}}{CE}$=$\frac{\frac{15}{4}}{\frac{9}{4}}$,
∴CE=$\frac{21}{20}$.
点评 本题考查了切线的性质:圆的切线垂直于经过切点的半径.运用切线的性质来进行计算或论证,常通过作辅助线连接圆心和切点,利用垂直构造直角三角形解决有关问题.也考查了圆周角定理和相似三角形的判定与性质.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
 如图所示,A,B,C三点分别是张庄,李庄,赵庄,现在计划建一个文化娱乐站,使这个文化娱乐站到这三个村庄的距离相等,假如你是设计师,你怎样选择建文化娱乐站的地址?(请用尺规作图,不写作法,保留作图痕迹)
如图所示,A,B,C三点分别是张庄,李庄,赵庄,现在计划建一个文化娱乐站,使这个文化娱乐站到这三个村庄的距离相等,假如你是设计师,你怎样选择建文化娱乐站的地址?(请用尺规作图,不写作法,保留作图痕迹)查看答案和解析>>
科目:初中数学 来源: 题型:选择题
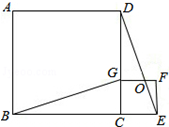 如图,四边形ABCD、CEFG都是正方形,点G在线段CD上,连接BG、DE,DE和FG相交于点O,设AB=a,CG=b(a>b).下列结论:①△BCG≌△DCE;②BG⊥DE;③$\frac{DG}{GC}=\frac{GO}{CE}$;④$\sqrt{\frac{{{S_{△EOF}}}}{{{S_{△BCG}}}}}=\frac{b}{a}$.其中结论正确的个数是( )
如图,四边形ABCD、CEFG都是正方形,点G在线段CD上,连接BG、DE,DE和FG相交于点O,设AB=a,CG=b(a>b).下列结论:①△BCG≌△DCE;②BG⊥DE;③$\frac{DG}{GC}=\frac{GO}{CE}$;④$\sqrt{\frac{{{S_{△EOF}}}}{{{S_{△BCG}}}}}=\frac{b}{a}$.其中结论正确的个数是( )| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (-a2)3=a6 | B. | 2$\sqrt{2}$+3$\sqrt{3}$=5$\sqrt{5}$ | C. | a6÷a3=a3 | D. | (a+4)(a-4)=a2-4 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. |  | B. |  | C. |  | D. |  |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
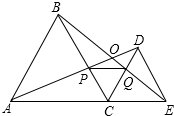 如图所示,C为线段AE上一动点(不与点A,E重合),在AE同侧分别作正△ABC和正△CDE,AD与BE交于点O,AD与BC交于点P,BE与CD交于点Q,连接PQ.以下四个结论:①△ACD≌△BCE;②AD=BE;③∠AOB=60°;④△CPQ是等边三角形.
如图所示,C为线段AE上一动点(不与点A,E重合),在AE同侧分别作正△ABC和正△CDE,AD与BE交于点O,AD与BC交于点P,BE与CD交于点Q,连接PQ.以下四个结论:①△ACD≌△BCE;②AD=BE;③∠AOB=60°;④△CPQ是等边三角形.| A. | ①②③④ | B. | ②③④ | C. | ①③④ | D. | ①②③ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
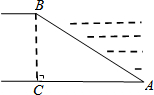 河堤的横断面如图所示,迎水坡AB=10米,迎水坡AB的坡比$1:\sqrt{3}$(坡比是坡面的垂直高度与水平宽度之比),则AC的长是( )
河堤的横断面如图所示,迎水坡AB=10米,迎水坡AB的坡比$1:\sqrt{3}$(坡比是坡面的垂直高度与水平宽度之比),则AC的长是( )| A. | 5米 | B. | $5\sqrt{3}$米 | C. | $\frac{{5\sqrt{3}}}{3}$米 | D. | $\frac{{10\sqrt{3}}}{3}$米 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com