
【题目】点O为直线AB上一点,将一直角三角板OMN的直角顶点放在点O处.射线OC平分∠MOB.
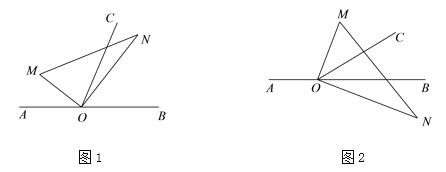
(1)如图1,若∠AOM=30°,求∠CON的度数;
(2)在图1中,若∠AOM=a,直接写出∠CON的度数(用含a的代数式表示);
(3)将图1中的直角三角板OMN绕顶点O顺时针旋转至图2的位置,一边OM在射线OB上方,另一边ON在直线AB的下方.
①探究∠AOM和∠CON的度数之间的关系,写出你的结论,并说明理由;
②当∠AOC=3∠BON时,求∠AOM的度数.
【答案】(1) 15°;(2) ∠CON=![]() a;(3) ①见解析;②144°.
a;(3) ①见解析;②144°.
【解析】
(1)根据角平分线的定义以及补角的定义,可求得∠CON的度数;
(2)可得∠CON=![]() a;
a;
(3) ①设∠AOM=a,可得![]() ,
,![]() ,可得∠AOM和∠CON的关系;
,可得∠AOM和∠CON的关系;
②由①知![]() ,
,![]() ,由∠AOC=3∠BON,可列方程
,由∠AOC=3∠BON,可列方程![]() ,可得答案.
,可得答案.
.
解:
(1)由已知得∠BOM=180°-∠AOM=150°,
又∠MON是直角,OC平分∠BOM,
所以∠CON=∠MON-![]() ∠BOM=90°-
∠BOM=90°-![]() ×150°=15°.
×150°=15°.
(2)∠CON=![]() a.
a.
(3)设∠AOM=a,则∠BOM=180°-a,
①∠AOM=2∠CON.
理由如下:
∵OC平分∠BOM,
∴![]()
∵![]()
∴![]()
∴![]()
②由①知![]()
![]()
![]()
∴![]()
解得![]()
∴![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】“魅力数学”社团活动时,张老师出示了如下问题:
如图①,已知四边形ABCD中,AC平分∠DAB,∠DAB=120°,∠B与∠D互补,试探究线段AB,AD,AC之间的数量关系;
小敏反复探索,不得其解,张老师提示道:“数学中常通过把一个问题特殊化来找到解题思路”,于是,小敏想,若将四边形ABCD特殊化,看如何解决问题:
(1)特殊情况入手
添加条件:“∠B=∠D”,如图②易知在Rt△CDA中,∠DCA=30°,所以,写出边AD与AC之间的数量关系,同理可得AB与AC的数量关系,由此得AB,AD,AC之间的数量关系;
(2)解决原来问题
受到(1)的启发,在原问题上,添加辅助线,过点C分别作AB,AD的垂线,垂足分别为E、F,如图③,请写出探究过程;
(3)解后反思
“一题多解”是数学解题的魅力之一,小敏在张老师的引导下,受探究结论的启发,结合图中的60°角,通过构造等边三角形,利用三角形全等同样解决了该问题,请在图①中作出辅助线,并简述你的探究过程.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知△ABC的三个顶点的坐标分别为A(-3,5),B(-2,1),C(-1,3).
(1)画出△ABC关于x轴的对称图形△A1B1C1;
(2)画出△A1B1C1沿x轴向右平移4个单位长度后得到的△A2B2C2;
(3)如果AC上有一点M(a,b)经过上述两次变换,那么对应A2C2上的点M2的坐标是 .

查看答案和解析>>
科目:初中数学 来源: 题型:
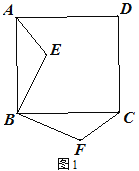
【题目】已知正方形ABC D,E为平面内任意一点,连接AE,BE,将△ABE绕点B顺时针旋转90°得到△BFC.
(1)如图1,求证:①![]() ;②
;②![]() .
.
(2)若![]() ,
,
① 如图2,点E在正方形内,连接EC,若![]() ,
, ![]() ,求
,求![]() 的长;
的长;
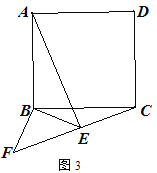
② 如图3,点E在正方形外,连接EF,若AB=6,当C、E、F在一条直线时,
求AE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】建立模型:
如图1,已知△ABC,AC=BC,∠C=90°,顶点C在直线l上.
操作:
过点A作AD⊥l于点D,过点B作BE⊥l于点E.求证:△CAD≌△BCE.
模型应用:
(1)如图2,在直角坐标系中,直线l1:y=![]() x+4与y轴交于点A,与x轴交于点B,将直线l1绕着点A顺时针旋转45°得到l2.求l2的函数表达式.
x+4与y轴交于点A,与x轴交于点B,将直线l1绕着点A顺时针旋转45°得到l2.求l2的函数表达式.
(2)如图3,在直角坐标系中,点B(8,6),作BA⊥y轴于点A,作BC⊥x轴于点C,P是线段BC上的一个动点,点Q(a,2a﹣6)位于第一象限内.问点A、P、Q能否构成以点Q为直角顶点的等腰直角三角形,若能,请求出此时a的值,若不能,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
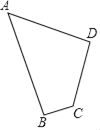
【题目】如图,四边形草坪ABCD中,∠B=90°,AB=24m,BC=7m,CD=15m,AD=20m.
(1)判断∠ADC是否是直角,并说明理由;
(2)试求四边形草坪ABCD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
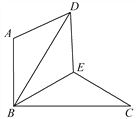
【题目】如图,△BAD是由△BEC在平面内绕点B旋转60°而得,且AB⊥BC,BE=CE,连接DE.
(1)求证:△BDE≌△BCE;
(2)试判断四边形ABED的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】温度的变化是人们在生活中经常谈论的话题,请你根据下图回答下列问题:
(1)上午9时的温度是多少?这一天的最高温度是多少?
(2)这一天的温差是多少?从最低温度到最高温度经过了多长时间?
(3)在什么时间范围内温度在下降?图中的A点表示的是什么?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形网格中小方格边长为1,请你根据所学的知识解决下面问题.
(1)求网格图中△ABC的面积.
(2)判断△ABC是什么形状?并所明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com