解答:
解:(1)∵抛物线y=ax
2+bx+3经过点B(-1,0)、C(3,0),
∴
,解得a=-1,b=2,
∴抛物线的解析式为:y=-x
2+2x+3.
(2)在直角梯形EFGH运动的过程中:
①四边形MOHE构成矩形的情形,如答图1所示:
此时边GH落在x轴上时,点G与点D重合.
由题意可知,EH,MO均与x轴垂直,且EH=MO=1,则此时四边形MOHE构成矩形.此时直角梯形EFGH平移的距离即为线段DF的长度.
过点F作FN⊥x轴于点N,则有FN=EH=1,FN∥y轴,
∴
=,即
=,解得DN=
.
在Rt△DFN中,由勾股定理得:DF=
=
=
,

∴t=
;
②四边形MOHE构成正方形的情形.
由答图1可知,OH=OD-DN-HN=4-
-1=
,即OH≠MO,
所以此种情形不存在;
③四边形MOHE构成菱形的情形,如答图2所示:
过点F作FN⊥x轴于点N,交GH于点T,过点H作HR⊥x轴于点R.易知FN∥y轴,RN=EF=FT=1,HR=TN.
设HR=x,则FN=FT+TN=FT+HR=1+x;
∵FN∥y轴,∴
=,即
=,解得DN=
(1+x).
∴OR=OD-RN-DN=4-1-
(1+x)=
-
x.
若四边形MOHE构成菱形,则OH=EH=1,
在Rt△ORH中,由勾股定理得:OR
2+HR
2=OH
2,
即:(
-
x)
2+x
2=1
2,解得x=
,
∴FN=1+x=
,DN=
(1+x)=
.
在Rt△DFN中,由勾股定理得:DF=
=
=3.
由此可见,四边形MOHE构成菱形的情形存在,此时直角梯形EFGH平移的距离即为线段DF的长度,
∴t=3.
综上所述,当t=
s时,四边形MOHE构成矩形;当t=3s时,四边形MOHE构成菱形.
(3)当t=
s或t=
s时,以A、A′、G、K为顶点的四边形为平行四边形.
简答如下:(注:本题并无要求写出解题过程,以下仅作参考)
由题意可知,AA′=2.以A、A′、G、K为顶点的四边形为平行四边形,则GK∥AA′,且GK=AA′=2.
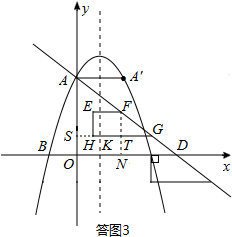
①当直角梯形位于△OAD内部时,如答图3所示:
过点H作HS⊥y轴于点S,由对称轴为x=1可得KS=1,∴SG=KS+GK=3.
由SG∥x轴,得
=,求得AS=
,∴OS=OA-AS=
,
∴FN=FT+TN=FT+OS=
,易知DN=
FN=
,
在Rt△FND中,由勾股定理求得DF=
;
②当直角梯形位于△OAD外部时,如答图4所示:

设GK与y轴交于点S,则GS=SK=1,AS=
,OS=OA+AS=
.
过点F作FN⊥x轴,交GH于点T,则FN=FT+NT=FT+OS=
.
在Rt△FGT中,FT=1,则TG=
,FG=
.
由TG∥x轴,∴
=,解得DF=
.
由于在以上两种情形中,直角梯形EFGH平移的距离均为线段DF的长度,则综上所述,当t=
s或t=
s时,以A、A′、G、K为顶点的四边形为平行四边形.

 解:(1)∵抛物线y=ax2+bx+3经过点B(-1,0)、C(3,0),
解:(1)∵抛物线y=ax2+bx+3经过点B(-1,0)、C(3,0),




 (2012•本溪)如图,△ABC是学生小金家附近的一块三角形绿化区的示意图,为增强体质,他每天早晨都沿着绿化区周边小路AB、BC、CA跑步(小路的宽度不计).观测得点B在点A的南偏东30°方向上,点C在点A的南偏东60°的方向上,点B在点C的北偏西75°方向上,AC间距离为400米.问小金沿三角形绿化区的周边小路跑一圈共跑了多少米?
(2012•本溪)如图,△ABC是学生小金家附近的一块三角形绿化区的示意图,为增强体质,他每天早晨都沿着绿化区周边小路AB、BC、CA跑步(小路的宽度不计).观测得点B在点A的南偏东30°方向上,点C在点A的南偏东60°的方向上,点B在点C的北偏西75°方向上,AC间距离为400米.问小金沿三角形绿化区的周边小路跑一圈共跑了多少米? (2012•本溪)如图,矩形ABCD中,点P、Q分别是边AD和BC的中点,沿过C点的直线折叠矩形ABCD使点B落在线段PQ上的点F处,折痕交AB边于点E,交线段PQ于点G,若BC长为3,则线段FG的长为
(2012•本溪)如图,矩形ABCD中,点P、Q分别是边AD和BC的中点,沿过C点的直线折叠矩形ABCD使点B落在线段PQ上的点F处,折痕交AB边于点E,交线段PQ于点G,若BC长为3,则线段FG的长为