
����Ŀ����ͼ����A��B��C��ʾij���ξ��������³�վ��λ�ã��߶�AB��BC��ʾ�����³�վ�ĸ��£���֪A��B��C������ͬһǦֱƽ���ڣ����ǵĺ��θ߶�AA�䣬BB�䣬CC��ֱ�Ϊ110�ף�310�ף�710�ף�����AB���¶�i1��1��2������BC���¶�i2��1��1������������³���·����Ҫ��A��Cֱ����һ�����£���ô����AC�ij����Ƕ����ף�(ע���¶�i��ָ�����Ǧֱ�߶���ˮƽ���ȵı�)

���𰸡�����AC�ij���Ϊ1 000�ף�
���������������������A��AE��CC���ڵ�E����BB���ڵ�F������B��BD��CC���ڵ�D���ֱ����AE��CE�����ù��ɶ������AC���ɣ�
�������������A��AE��CC���ڵ�E����BB���ڵ�F������B��BD��CC���ڵ�D��
����AFB����BDC����AEC����ֱ�������Σ��ı���AA��B��F��BB��C��D��BFED���Ǿ��Σ�
��BF=BB��-B��F=BB��-AA��=310-110=200��
CD=CC��-C��D=CC��-BB��=710-310=400��
��i1=1��2��i2=1��1��
��AF=2BF=400��BD=CD=400��
����EF=BD=400��DE=BF=200��
��AE=AF+EF=800��CE=CD+DE=600��
����Rt��AEC�У�AC=![]() ���ף���
���ף���
�𣺸���AC�ij�����1000�ף�
���㣺��ֱ�������ε�Ӧ��-�¶��½����⣮
�����͡������
��������
24
����Ŀ����ͼ�٣�ABΪ��Բ��ֱ����OΪԲ�ģ�CΪԲ����һ�㣬AD��ֱ�ڹ�C������ߣ�����ΪD��AB���ӳ��߽�ֱ��CD�ڵ�E.
(1)��֤��ACƽ�֡�DAB��
(2)��AB��4��BΪOE���е㣬CF��AB������Ϊ��F����CF�ij���
(3)��ͼ�ڣ�����OD��AC�ڵ�G����![]() ����sinE��ֵ��
����sinE��ֵ��

���𰸡�(1)֤����������(2)CF��![]() ��(3) sinE��
��(3) sinE��![]() .
.
����������������1������OC����ƽ���ߵ��ж������������Լ��������еĵȽǶԵȱߵ�ԭ��������֤����2���ɣ�1���н��ۣ���������ǵ����Ǻ���ֵ�������E=30��CF�ij��ȡ���3������OC������֤����OCG�ס�DAG����OCE�ס�DAE���������������εĶ�Ӧ�߳ɱ������ɵ�EO��AO�ı�����ϵ������ΪOC=OA��������RT��OCE�������Ǻ����Ķ��弴����⡣
���������(1)����OC����ͼ��.��OC�а�ԲO��C����OC��DC����AD��CD.��OC��AD.���OCA����DAC.��OC��OA�����OAC����ACO.���DAC����CAO����ACƽ�֡�DAB.
(2)��Rt��OCE����OC��OB��![]() OE�����E��30��.
OE�����E��30��.
����Rt��OCF�У�CF��OC��sin60�㣽2��![]() ��
��![]() .
.
(3)����OC����ͼ��.��CO��AD�����CGO�ס�AGD.��![]() ��
��![]() ��
��![]() .������CO��AO��3k����AD��4k.�֡�COE�ס�DAE����
.������CO��AO��3k����AD��4k.�֡�COE�ס�DAE����![]() ��
��![]() ��
��![]() ��
��![]() .��EO��9k.��Rt��COE��sinE��
.��EO��9k.��Rt��COE��sinE��![]() ��
��![]() ��
��![]() .
.




| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
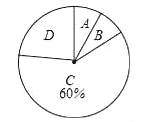
����Ŀ������10����ij��˾�����ȡ������a��������������������������갴�������ɼ��ֳ���A��B��C��D�ĸ��ȼ�����������ͼ�в�������ͳ��ͼ����

����������Ϣ�������������
��1����a��ֵ��
��2��������ͳ��ͼ������B�ȼ��������ε�Բ�ĽǵĴ�С��������öȡ��֡����ʾ��
��3���������ɼ�������80�ֵ�����������ѡ2�ҽ���Ӫ��������������������һ����A�ȼ��ĸ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
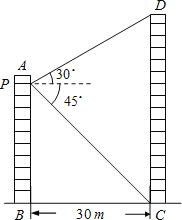
����Ŀ����ͼ��ʾ������������AB��CD��ˮƽ����Ϊ30m������ͬѧס�ڽ�����AB��10¥P�ң����۲⽨����CD¥�Ķ���D��������Ϊ30������õײ�C���ĸ���Ϊ45����������CD�ĸ߶ȣ���![]() ȡ1.73�����������������
ȡ1.73�����������������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����DΪ����CB��һ�����Ҳ����B��C�غ���DE��AB��ֱ��AC�ڵ�E��DF��AC��ֱ��AB�ڵ�F.�������������ͼ���������EDF���BAC��������ϵ����˵������.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
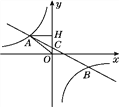
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�һ�κ���y��ax��b(a��0)��ͼ���뷴��������y��![]() (k��0)��ͼ���ڵڶ����������ڵ�A��B���㣬��y�ύ��C�㣬����A��AH��y�ᣬ����ΪH��OH��3��tan��AOH��
(k��0)��ͼ���ڵڶ����������ڵ�A��B���㣬��y�ύ��C�㣬����A��AH��y�ᣬ����ΪH��OH��3��tan��AOH��![]() ����B������Ϊ(m����2)��
����B������Ϊ(m����2)��
(1)���AHO���ܳ���
(2)��÷�����������һ�κ����Ľ���ʽ��
���𰸡�(1)��AHO���ܳ�Ϊ12��(2) �����������Ľ���ʽΪy��![]() ��һ�κ����Ľ���ʽΪy����
��һ�κ����Ľ���ʽΪy����![]() x��1.
x��1.
���������������: ��1���������к������ɵ�AH�ij������ݹ��ɶ������ɵ�AO�ij������������ε��ܳ����ɵô𰸣�
��2�����ݴ���ϵ�������ɵú�������ʽ��
�����������1����OH=3��tan��AOH=![]() ����
����
AH=4����A��-4��3����
�ɹ��ɶ�������
AO=![]() =5��
=5��
��AHO���ܳ�=AO+AH+OH=3+4+5=12��
��2����A���������y=![]() ��k��0������
��k��0������
k=-4��3=-12��
�����������Ľ���ʽΪy=![]() ��
��
��y=-2ʱ��-2=![]() �����x=6����B��6��-2����
�����x=6����B��6��-2����
��A��B���������y=ax+b����
![]() ��
��
���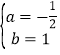 ��
��
һ�κ����Ľ���ʽΪy=-![]() x+1��
x+1��
���㣺������������һ�κ����Ľ������⣮
�����͡������
��������
23
����Ŀ����ͼ����A��B��C��ʾij���ξ��������³�վ��λ�ã��߶�AB��BC��ʾ�����³�վ�ĸ��£���֪A��B��C������ͬһǦֱƽ���ڣ����ǵĺ��θ߶�AA�䣬BB�䣬CC��ֱ�Ϊ110�ף�310�ף�710�ף�����AB���¶�i1��1��2������BC���¶�i2��1��1������������³���·����Ҫ��A��Cֱ����һ�����£���ô����AC�ij����Ƕ����ף�(ע���¶�i��ָ�����Ǧֱ�߶���ˮƽ���ȵı�)
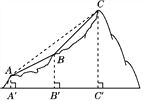
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����һ�麬30��ǵ�ֱ�����ǰ�OAB��ֱ�DZ�BO�ij�ǡ����һ�����ֱ�����ǰ�ODC��б��OC�ij���ȣ������������ǰ������ƽ��ֱ������ϵ�У���OB��3![]() .
.
(1)��ij������������ͼ���һ����֧ǡ�þ�����A������������������Ľ���ʽ��
(2)���Ѻ�30��ǵ�ֱ�����ǰ��Ƶ�O��˳ʱ�뷽����ת��б��OAǡ������x���ϣ���A���ڵ�A�䴦������ͼ����Ӱ���ֵ������(���������)
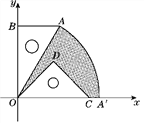
���𰸡�(1)�����������Ľ���ʽΪy��![]() ��(2)S��Ӱ��6�У�
��(2)S��Ӱ��6�У�![]() .
.
����������������1������tan30��=![]() �����AB���������OA���ó�A�����꣬���A��˫���ߵĽ���ʽ��y=
�����AB���������OA���ó�A�����꣬���A��˫���ߵĽ���ʽ��y=![]() ����A���������������ɣ���2�������AOA�䣬�������ε������ʽ�������AOA�����������OD��DC���������ODC������������������𰸣�
����A���������������ɣ���2�������AOA�䣬�������ε������ʽ�������AOA�����������OD��DC���������ODC������������������𰸣�
���������
(1)��Rt��OBA�У���AOB��30�㣬OB��3![]() ��
��
��AB��OB��tan 30�㣽3.
���A������Ϊ(3��3![]() )��
)��
�跴���������Ľ���ʽΪy��![]() (k��0)��
(k��0)��
��3![]() ��
��![]() ����k��9
����k��9![]() ������������������Ľ���ʽΪy��
������������������Ľ���ʽΪy��![]() .
.
(2)��Rt��OBA�У���AOB��30�㣬AB��3��
sin ��AOB��![]() ����sin 30�㣽
����sin 30�㣽![]() ��
��
��OA��6.
������ã���AOC��60�㣬S����AOA����![]() ��6��.
��6��.
��Rt��OCD�У���DOC��45�㣬OC��OB��3![]() ��
��
��OD��OC��cos 45�㣽3![]() ��
��![]() ��
��![]() .
.
��S��ODC��![]() OD2��
OD2��![]()
![]() ��
��![]() .
.
��S��Ӱ��S����AOA����S��ODC��6����![]() .
.
�㾦�����⿼���˹��ɶ���������ϵ������������ʽ������ǵ����Ǻ���ֵ�����ε���������������ε����ʣ����������е��⣬�ѶȲ����������ͼ�ε������ʾ�ɶ������ͼ�ε����֮���ǽ����Ĺؼ�.
�����͡������
��������
26
����Ŀ������ABCDһ����AD��8��������ABCD�۵���ʹ�õ�B����CD���ϵĵ�P����
(1)��ͼ�٣���֪�ۺ����BC���ڵ�O������AP��OP��OA.
�� ��֤����OCP�ס�PDA��
�� ����OCP���PDA�������Ϊ1:4�����AB�ij���
(2)��ͼ�ڣ���(1)�������£���ȥAO��OP������BP.����M���߶�AP��(�����P��A�غ�)������N���߶�AB���ӳ����ϣ���BN��PM������MN��PB�ڵ�F����ME��BP�ڵ�E.���ʶ���M��N���ƶ��Ĺ����У��߶�EF�ij����Ƿ����仯�������䣬����߶�EF�ij��ȣ����仯��˵�����ɣ�
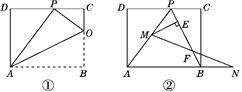
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�������������У�ÿ��С�����εı߳�Ϊ1����������һ�������ABC���������εĶ��㶼�ڸ���ϣ�
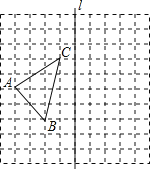
��1����ͼ��������ABC����ֱ��1�ԳƵ���A1B1C1����Ҫ��A��A1��B��B1��C��C1���Ӧ����
��2���ڵڣ�1���ʵĽ���£�����BB1��CC1�����ı���BB1C1C�������
��3����ͼ��������ABC���ڵ�C�����ĶԳƵ���A2CB2��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����9�֣���ͼ��һ�κ���y=kx+b�뷴��������![]() ��ͼ����A��2��3����B����3��n�����㣮
��ͼ����A��2��3����B����3��n�����㣮
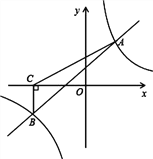
��1����һ�κ����뷴���������Ľ���ʽ��
��2������������������ֱ��д������ʽkx+b��![]() �Ľ⼯��
�Ľ⼯��
��3������B��BC��x�ᣬ����ΪC�����ABC�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����BAD������BEC��ƽ�����Ƶ�B��ת60�����ã���AB��BC��BE��CE������DE.
��1����֤����BDE�ա�BCE��
��2�����ж��ı���ABED����״����˵�����ɣ�

�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com