
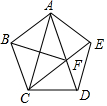
 如图,正五边形ABCDE中.连接AC,AD,CE,CE交AD于点F,连接BF.下列说怯正确的是①③④(将所有正确说法的序号填写在横线上).①△ACD的周长大于4CD;②FC平分∠BFD:③四边形ABCF是菱形;④CD2=EF•CE.
如图,正五边形ABCDE中.连接AC,AD,CE,CE交AD于点F,连接BF.下列说怯正确的是①③④(将所有正确说法的序号填写在横线上).①△ACD的周长大于4CD;②FC平分∠BFD:③四边形ABCF是菱形;④CD2=EF•CE. 分析 由四边形ABCF是菱形,易得∠AFE=∠DEF,∠AFB=∠EDF,由正五边形的性质得∠ABC=108°,∠CFB=∠CBF=∠AFB=54°,∠CFD=72°,可得∠BFC≠∠CFD,证得结论;首先根据是正五边形的性质得到AB=BC=CD=DE=AE,AB∥CE,BC∥AD,AB=BC,根据有一组邻边相等的平行四边形是菱形即可证;根据正五边形的性质和等腰三角形的性质∠BAC=∠BCA=∠AED=∠EDA=∠DCE=∠CED=36°,根据相似三角形的判定和性质即可得到结论.
解答 解:∵四边形ABCF是菱形,
∴∠AFE=∠DEF,∠AFB=∠EDF,
∵正五边形ABCDE∠ABC=108°,∠CFB=∠CBF=∠AFB=54°,
∴∠CFD=72°,
∴∠BFC≠∠CFD,
故②错误;
∵五边形ABCDE是正五边形,
∴AB=BC=CD=DE=AE,AB∥CE,BC∥AD,
∴四边形AEDF是平行四边形,
∵AB=BC,
∴四边形ABCF是菱形,
故③正确;
由正五边形的性质可得AC=AD,AB=CD,CD=DE,∠FED=∠FDE,
∴EF=FD,
∵四边形ABCF是菱形,
∴AB=BC=CF=FA,
∴AF=CD,
∴△ACD的周长=2AD+CD=3CD+2FD,
∵2FD=FD+EF>DE,
∴2FD>CD,
∴△ACD的周长=2AD+CD=3CD+2FD>4CD,
故①正确;
∵正五边形ABCDE中,∠BAE=∠BCD=∠EDC=108°,AB=BC=CD=AE=DE,
∴∠BAC=∠BCA=∠AED=∠EDA=∠DCE=∠CED=36°,
∴△ECD∽△DEF,
∴$\frac{DE}{EF}=\frac{CE}{DE}$,
∴DE2=EF•CE,
∵CD=DE,
∴CD2=EF•CE.故④正确;
故答案为:①③④.
点评 本题考查了相似三角形的判定和性质,正五边形的性质,综合考察的知识点较多,解答本题注意已经证明的结论,可以直接拿来使用.


 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案 一线名师权威作业本系列答案
一线名师权威作业本系列答案科目:初中数学 来源: 题型:选择题
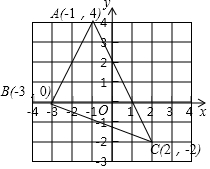 如图,三角形ABC中任意一点P(x0,y0)经平移后对应点为P1(x0+3,y0-1),将三角形ABC作同样的平移得到三角形A1B1C1,则A1的坐标是( )
如图,三角形ABC中任意一点P(x0,y0)经平移后对应点为P1(x0+3,y0-1),将三角形ABC作同样的平移得到三角形A1B1C1,则A1的坐标是( )| A. | (-4,3) | B. | (-4,5) | C. | (2,3) | D. | (2,5) |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{2}$+$\sqrt{3}$=$\sqrt{5}$ | B. | 3$\sqrt{2}$-$\sqrt{2}$=3 | C. | $\sqrt{3}$×$\sqrt{5}$=$\sqrt{15}$ | D. | $\sqrt{(-3)^{2}}$=-3 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
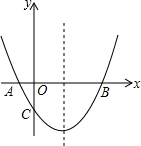 如图,抛物线经过A(-1,0),B(5,0),C(0,-$\frac{5}{2}$)三点.
如图,抛物线经过A(-1,0),B(5,0),C(0,-$\frac{5}{2}$)三点.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (1)和(4) | B. | (2)和(3) | C. | (1)和(2) | D. | (3)和(4) |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题

| A. | 2017 | B. | 4034 | C. | 6051 | D. | 8068 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com