
分析 先把分子、分母进行因式分解,再通分,然后把除法转化成乘法,再进行约分,最后把求出x的值代入原式,进行计算即可.
解答 解:$\frac{{x}^{2}-1}{{x}^{2}-x}$$÷(2+\frac{{x}^{2}+1}{x})$=$\frac{(x+1)(x-1)}{x(x-1)}$÷($\frac{2x}{x}$+$\frac{{x}^{2}+1}{x}$)=$\frac{x+1}{x}$÷$\frac{(x+1)^{2}}{x}$=$\frac{x+1}{x}$×$\frac{x}{(x+1)^{2}}$=$\frac{1}{x+1}$,
∵x=2sin45°-1=2×$\frac{\sqrt{2}}{2}$-1=$\sqrt{2}$-1,
∴原式=$\frac{1}{\sqrt{2}-1+1}$=$\frac{1}{\sqrt{2}}$=$\frac{\sqrt{2}}{2}$.
点评 此题考查了分式的化简求值,用到的知识点是分式的化简步骤和特殊角的三角函数值,关键是把分式化到最简,然后代值计算.


 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
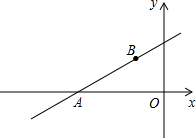 如图,直线l:y=$\frac{{\sqrt{3}}}{3}$x+m与x轴交于A点,且经过点B(-$\sqrt{3}$,2).已知抛物线C:y=ax2+bx+9与x轴只有一个公共点,恰为A点.
如图,直线l:y=$\frac{{\sqrt{3}}}{3}$x+m与x轴交于A点,且经过点B(-$\sqrt{3}$,2).已知抛物线C:y=ax2+bx+9与x轴只有一个公共点,恰为A点.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| x | 1 | 2 | 3 | 4 |
| y | 0 | 1 | 2 | 3 |
| x | -2 | 2 | 4 | 6 |
| y | 0 | 2 | 3 | 4 |
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com