
如图是二次函数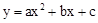 图象的一部分,其对称轴为x=﹣1,且过点(﹣3,0).下列说法:①abc<0;②2a﹣b=0;③4a+2b+c<0;④若(﹣5,y1),(
图象的一部分,其对称轴为x=﹣1,且过点(﹣3,0).下列说法:①abc<0;②2a﹣b=0;③4a+2b+c<0;④若(﹣5,y1),(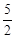 ,y2)是抛物线上两点,则
,y2)是抛物线上两点,则
y1>y2.其中说法正确的是【 】
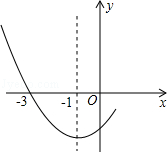
A.①② B.②③ C.①②④ D.②③④
C。
【解析】∵二次函数的图象的开口向上,∴a>0。
∵二次函数的图象y轴的交点在y轴的负半轴上,∴c<0。
∵二次函数图象的对称轴是直线x=﹣1,∴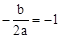 。∴b=2a>0。
。∴b=2a>0。
∴abc<0,因此说法①正确。
∵2a﹣b=2a﹣2a=0,因此说法②正确。
∵二次函数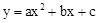 图象的一部分,其对称轴为x=﹣1,且过点(﹣3,0),
图象的一部分,其对称轴为x=﹣1,且过点(﹣3,0),
∴图象与x轴的另一个交点的坐标是(1,0)。
∴把x=2代入y=ax2+bx+c得:y=4a+2b+c>0,因此说法③错误。
∵二次函数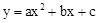 图象的对称轴为x=﹣1,
图象的对称轴为x=﹣1,
∴点(﹣5,y1)关于对称轴的对称点的坐标是(3,y1),
∵当x>﹣1时,y随x的增大而增大,而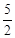 <3
<3
∴y2<y1,因此说法④正确。
综上所述,说法正确的是①②④。故选C。


 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案科目:初中数学 来源: 题型:
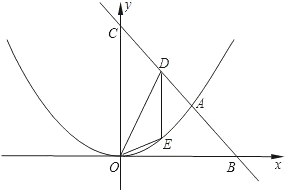 象经过点A和点B(6,0).
象经过点A和点B(6,0).查看答案和解析>>
科目:初中数学 来源: 题型:
已知如图,二次函数![]()
![]() 图象的顶点为
图象的顶点为![]() ,与
,与![]() 轴交于
轴交于![]() 、
、![]() 两点(
两点(![]() 在
在![]() 点右侧),点
点右侧),点![]() 、
、![]() 关于直线
关于直线![]() :
:![]() 对称.
对称.

(1)求![]() 、
、![]() 两点坐标,并证明点
两点坐标,并证明点![]() 在直线
在直线![]() 上;
上;
(2)求二次函数解析式;
(3)过点![]() 作直线
作直线![]() ∥
∥![]() 交直线
交直线![]() 于
于![]() 点,
点,![]() 、
、![]() 分别为直线
分别为直线![]() 和直线
和直线![]() 上的两个动点,连接
上的两个动点,连接![]() 、
、![]() 、
、![]() ,求
,求![]() 和的最小值.
和的最小值.
【解析】(1)根据一元二次方程求得A点坐标,代入直线求证,(2)通过点H、B关于直线L对称,求得H的坐标,从而解出二次函数的解析式,(3)先求出HN+MN的最小值是MB, 再求出BM+MK的最小值是BQ,即![]() 和的最小值
和的最小值
查看答案和解析>>
科目:初中数学 来源:2013-2014学年浙江临安於潜二中九年级数学上学期期末模拟数学试卷(解析版) 题型:填空题
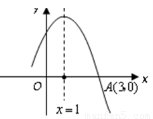
如图是二次函数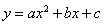 图象的一部分,图象过点
图象的一部分,图象过点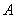 (3,0),且对称轴为
(3,0),且对称轴为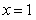 ,给出下列四个结论:①
,给出下列四个结论:① ;②
;②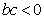 ;③
;③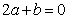 ;④
;④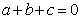 ,其中正确结论的序号是___________.(把你认为正确的序号都写上)
,其中正确结论的序号是___________.(把你认为正确的序号都写上)
查看答案和解析>>
科目:初中数学 来源:2011-2012学年江苏省无锡市新区九年级下学期期中考试数学卷(解析版) 题型:解答题
已知如图,二次函数
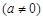 图象的顶点为
图象的顶点为 ,与
,与 轴交于
轴交于 、
、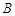 两点(
两点(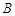 在
在 点右侧),点
点右侧),点 、
、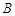 关于直线
关于直线 :
: 对称.
对称.

(1)求 、
、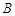 两点坐标,并证明点
两点坐标,并证明点 在直线
在直线 上;
上;
(2)求二次函数解析式;
(3)过点 作直线
作直线 ∥
∥ 交直线
交直线 于
于 点,
点, 、
、 分别为直线
分别为直线 和直线
和直线 上的两个动点,连接
上的两个动点,连接 、
、 、
、 ,求
,求 和的最小值.
和的最小值.
【解析】(1)根据一元二次方程求得A点坐标,代入直线求证,(2)通过点H、B关于直线L对称,求得H的坐标,从而解出二次函数的解析式,(3)先求出HN+MN的最小值是MB, 再求出BM+MK的最小值是BQ,即 和的最小值
和的最小值
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com