
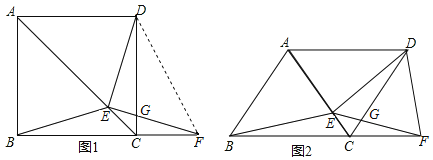
【题目】如图1,在正方形![]() 中,
中,![]() 是对角线
是对角线![]() 上的一点,点
上的一点,点![]() 在
在![]() 的延长线上,
的延长线上,![]() 交
交![]() 于
于![]() ,
,![]() .
.
(1)求证:![]() ;
;
(2)连接![]() ,若
,若![]() ,求
,求![]() ;
;
(3)如图2,若把正方形![]() 改为菱形
改为菱形![]() ,其他条件不变,当
,其他条件不变,当![]() 时,猜想
时,猜想![]() 与
与![]() 的数量关系,并证明你的猜想.
的数量关系,并证明你的猜想.
【答案】(1)证明见解析;(2)BE=![]() ;(3)BE=DF,理由见解析
;(3)BE=DF,理由见解析
【解析】
(1)根据正方形的性质证明△BCE≌△DCE即可;
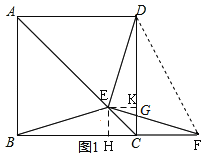
(2)过E作EK⊥DC于K,EH⊥BC于H,构建正方形EHCK,通过证明Rt△DEK≌Rt△FEH得出△DEF是等腰直角三角形,进而得解;
(3)先证明△BCE≌△DCE,得∠EBC=∠EDC,BE=ED,根据三角形内角和可得∠DEF=∠DCF=∠ABC=60°,进而得出△DEF是等边三角形,可得结论.
(1)证明:∵四边形ABCD是正方形,
∴BC=DC,∠BCE=∠DCE,
∵EC=EC,
∴△BCE≌△DCE,
∴BE=ED,
∵EF=ED,
∴EB=EF;
(2)解:如图1,过E作EK⊥DC于K,EH⊥BC于H,
∴∠EKC=∠EHC=∠BCD=90°,
∴四边形EHCK是矩形,
∵∠ECH=45°,
∴△EHC是等腰直角三角形,
∴EH=CH,
∴矩形EHCK是正方形,
∴EK=EH,
∴Rt△DEK≌Rt△FEH,
∴∠DEK=∠FEH,
∴∠DEK+∠FEK=∠FEH+∠FEK,
∴∠DEF=90°,
∴△DEF是等腰直角三角形,
∵DF=2,
∴DE=![]() ,
,
∴BE=![]() ;
;
(3)解:BE=DF,理由是:
∵四边形ABCD是菱形,
∴BC=DC,∠BCE=∠DCE,
∵EC=EC,
∴△BCE≌△DCE,
∴∠EBC=∠EDC,BE=ED,
∵EF=ED,
∴EB=EF,
∴∠EBC=∠EFC,
∴∠EDC=∠EFC,
∵∠EGD=∠CGF,
∴∠DEF=∠DCF=∠ABC=60°,
∴△DEF是等边三角形,
∴DF=EF,
∴BE=DF.


 小学教材完全解读系列答案
小学教材完全解读系列答案科目:初中数学 来源: 题型:
【题目】如图,过点P作PA,PB,分别与以OA为半径的半圆切于A,B,延长AO交切线PB于点C,交半圆与于点D.
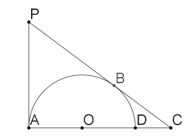
(1)若PC=5,AC=4,求BC的长;
(2)设DC:AD=1:2,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小李在学习了定理“直角三角形斜边上的中线等于斜边的一半”之后做了如下思考,请你帮他完成如下问题:
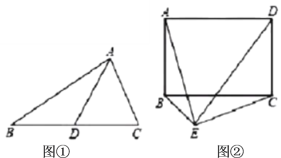
(1)他认为该定理有逆定理:“如果一个三角形某条边上的中线等于该边长的一半,那么这个三角形是直角三角形”应该成立.即如图①,在![]() 中,
中,![]() 是
是![]() 边上的中线,若
边上的中线,若![]() ,求证:
,求证:![]() .
.
(2)如图②,已知矩形![]() ,如果在矩形外存在一点
,如果在矩形外存在一点![]() ,使得
,使得![]() ,求证:
,求证:![]() .(可以直接用第(1)问的结论)
.(可以直接用第(1)问的结论)
(3)在第(2)问的条件下,如果![]() 恰好是等边三角形,请求出此时矩形的两条邻边
恰好是等边三角形,请求出此时矩形的两条邻边![]() 与
与![]() 的数量关系.
的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
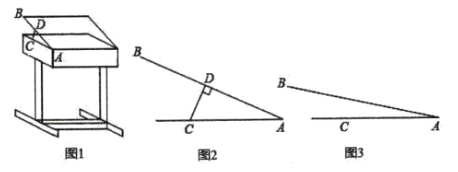
【题目】某课桌生产厂家研究发现,倾斜12°至24°的桌面有利于学生保持躯体自然姿势.根据这一研究,厂家决定将水平桌面做成可调节角度得桌面.新桌面的设计图如图1,![]() 可绕点
可绕点![]() 旋转,在点
旋转,在点![]() 处安装一根长度一定且
处安装一根长度一定且![]() 处固定,可旋转的支撑臂
处固定,可旋转的支撑臂![]() ,
,![]() .
.
(1)如图2,当![]() 时,
时,![]() ,求支撑臂
,求支撑臂![]() 的长;
的长;
(2)如图3,当![]() 时,求
时,求![]() 的长.(结果保留根号)
的长.(结果保留根号)
(参考数据:![]() ,
,![]() ,
,![]() ,
,![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
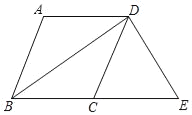
【题目】如图,在四边形ABCD中,AD∥BC,BA=BC,BD平分∠ABC.
(1)求证:四边形ABCD是菱形;
(2)过点D作DE⊥BD,交BC的延长线于点E,若BC=5,BD=8,求四边形ABED的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,一次函数![]() 的图象与反比例函数
的图象与反比例函数![]() 的图象交于点A (2,4)和B(-4,m).
的图象交于点A (2,4)和B(-4,m).
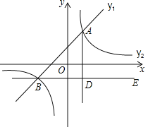
(1)求一次函数和反比例函数的表达式;
(2)请直接写出y1>y2时,x的取值范围;
(3)过点B作BE∥x轴,AD⊥BE于点D,点C是直线BE上一点,若AC=2CD,求点C的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】由甲、乙两个工程队承包某校校园绿化工程,甲、乙两队单独完成这项工程所需时间比是3︰2,两队合做6天可以完成.
(1)求两队单独完成此项工程各需多少天?
(2)此项工程由甲、乙两队合做6天完成任务后,学校付给他们20000元报酬,若
按各自完成的工程量分配这笔钱,问甲、乙两队各得到多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程![]() .
.
(1)求证:无论k取何实数值,方程总有实数根;
(2)若等腰△ABC的一边长a=6,另两边长b、c恰好是这个方程的两个根,求此三角形的三边长?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等边△ABC中,AB=6,D是AC的中点,E是BC延长线上的一点,CE=CD,DF⊥BE,垂足为F.
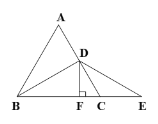
(1)求证:BF=EF;
(2)求△BDE的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com