
【题目】心理学家研究发现,一般情况下,一节课40分钟中,学生的注意力随教师讲课时间的变化而变化.开始上课时,学生的注意力逐步增强,中间有一段时间学生的注意力保持较为理想的稳定状态,随后学生的注意力开始分散.经过实验分析可知,学生的注意力指标数y随时间x(分钟)的变化规律如图所示(其中AB、BC分别为线段,CD为双曲线的一部分),请问:
如果有一道数学综合题,需要讲19分钟,为了效果较好,要求学生的注意力指标数最低达到36,那么经过适当安排,老师可否在学生注意力达到较为理想的稳定状态下讲解完这道题目?
你的结论是 (填写“可以”或“不可以”),理由是 (请通过你计算所得的数据说明理由).
【答案】可以;设线段AB所在的直线的解析式为![]() ,把B(10,40)代入得,
,把B(10,40)代入得,![]() =2,∴AB解析式为:
=2,∴AB解析式为:![]() =2x+20(0≤x≤10).设C、D所在双曲线的解析式为
=2x+20(0≤x≤10).设C、D所在双曲线的解析式为![]() ,把C(25,40)代入得,
,把C(25,40)代入得,![]() =1000,∴曲线CD的解析式为:
=1000,∴曲线CD的解析式为:![]() =
=![]() (x≥25);令
(x≥25);令![]() =36,∴36=2x+20,∴
=36,∴36=2x+20,∴![]() =8,令
=8,令![]() =36,∴36=
=36,∴36=![]() ,∴
,∴![]() ≈27.8,∵27.8﹣8=19.8>19,∴经过适当安排,老师能在学生注意力达到所需的状态下讲解完这道题目.
≈27.8,∵27.8﹣8=19.8>19,∴经过适当安排,老师能在学生注意力达到所需的状态下讲解完这道题目.
【解析】
试题分析:先用待定系数法分别求出AB和CD的函数表达式,分别求出注意力指数为36时的两个时间,再将两时间之差和19比较,大于19则能讲完,否则不能.设线段AB所在的直线的解析式为![]() ,把B(10,40)代入得,
,把B(10,40)代入得,![]() =2,∴AB解析式为:
=2,∴AB解析式为:![]() =2x+20(0≤x≤10).设C、D所在双曲线的解析式为
=2x+20(0≤x≤10).设C、D所在双曲线的解析式为![]() ,把C(25,40)代入得,
,把C(25,40)代入得,![]() =1000,∴曲线CD的解析式为:
=1000,∴曲线CD的解析式为:![]() =
=![]() (x≥25);令
(x≥25);令![]() =36,∴36=2x+20,∴
=36,∴36=2x+20,∴![]() =8,令
=8,令![]() =36,∴36=
=36,∴36=![]() ,∴
,∴![]() ≈27.8,∵27.8﹣8=19.8>19,∴经过适当安排,老师能在学生注意力达到所需的状态下讲解完这道题目.
≈27.8,∵27.8﹣8=19.8>19,∴经过适当安排,老师能在学生注意力达到所需的状态下讲解完这道题目.



科目:初中数学 来源: 题型:
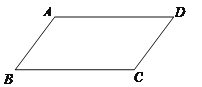
【题目】如图,已知AD∥BC,要使四边形ABCD为平行四边形,需要增加的一个条是:_____.(只填一个你认为正确的条件即可,不添加任何线段与字母)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,给正五边形的顶点依次编号为1,2,3,4,5.若从某一顶点开始,沿正五边形的边顺时针方向行走,顶点编号的数字是几,就走几个边长,则称这种走法为一次“移位”.如:小宇在编号为3的顶点上时,那么他应走3个边长,即从3→4→5→1为第一次“移位”,这时他到达编号为1的顶点;然后从1→2为第二次“移位”.若小宇从编号为2的顶点开始,第81次“移位”后,则他所处顶点的编号是 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在四边形ABCD中,AD∥BC,分别添加下列条件:①AB∥CD;②AB=CD;③AD=BC;④∠B=∠D;⑤∠A=∠C,其中能使四边形ABCD成为平行四边形的条件有( )
A. 5个 B. 4个 C. 3个 D. 2个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线![]() 与
与![]() 轴、
轴、![]() 轴分别相交于点A和B.
轴分别相交于点A和B.
(1)直接写出坐标:点A ,点B ;
(2)以线段AB为一边在第一象限内作□ABCD,其顶点D(![]() ,
, ![]() )在双曲线
)在双曲线![]() (
(![]() >
>![]() )上.
)上.
①求证:四边形ABCD是正方形;
②试探索:将正方形ABCD沿![]() 轴向左平移多少个单位长度时,点C恰好落在双曲线
轴向左平移多少个单位长度时,点C恰好落在双曲线![]() (
(![]() >
>![]() )上.
)上.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 下列长度的三条线段,能组成三角形的是( )
A.3cm,5cm,7cmB.7cm,7cm,14cmC.4cm,5cm,9cmD.2cm,1cm,3cm
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com