
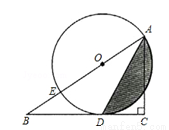
如图,已知直线PA交⊙O于A、B两点,AE是⊙O的直径,点C为⊙O上一点,且AC平分∠PAE,过C作CD⊥PA,垂足为D.
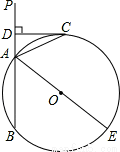
(1)求证:CD为⊙O的切线;
(2)若DC=4,AC=5,求⊙O的直径的AE.
(1)证明见解析;(2) .
.
【解析】
试题分析:(1)连接OC,根据OA=OC推出∠OCA=∠OAC,根据角平分线得出∠OCA=∠OAC=∠CAP,推出OC∥AP,得出OC⊥CD,根据切线的判定推出即可;
(2)过O作OM⊥AB于M,得出矩形OMDC,推出OM=CD,OC=AM+AD,求出AM的长,利用勾股定理求出AD的长,设圆的半径为x,则AM=x-AD,再根据勾股定理列方程,求出x的值即可求出⊙O的半径,从而求出⊙O的直径的AE.
试题解析:(1)证明:连接OC.

∵OC=OA,
∴∠OAC=∠OCA.
∵AC平分∠PAE,
∴∠DAC=∠OAC,
∴∠DAC=∠OCA,
∴AD∥OC.
∵CD⊥PA,
∴∠ADC=∠OCD=90°,
即 CD⊥OC,点C在⊙O上,
∴CD是⊙O的切线.
(2)【解析】
过O作OM⊥AB于M.即∠OMA=90°,
∵∠MDC=∠OMA=∠DCO=90°,
∴四边形DMOC是矩形,
∴OC=DM,OM=CD=4.
∵DC=4,AC=5,
∴AD=3,
设圆的半径为x,则AM=x-AD=x-3,
∵在Rt△AMO中,∠AMO=90°,根据勾股定理得:AO2=AM2+OM2.
∴x2=(x-3)2+42,
∴x=
∴⊙O的半径是 ,
,
∴⊙O的直径的AE=2× =
= .
.
考点:1.切线的判定;2.角平分线的性质;3.圆周角定理;4.相似三角形的判定与性质.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源:2014-2015学年江苏省宜兴市九年级11月阶段性检测数学试卷(解析版) 题型:选择题
如图,四边形ABCD中,DC∥AB,BC=1,AB=AC=AD=2,则BD的长为( )

A.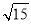 B.
B.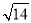 C.3
C.3 D.2
D.2
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省盐城市盐都区九年级上学期期末考试数学试卷(解析版) 题型:解答题
(本题满分10分)如图,在Rt△ABC中,∠C=90°,点E在斜边AB上,以AE为直径的⊙O与BC相切于点D.若BE=6,BD=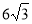 .
.
(1)求⊙O的半径;
(2)求图中阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省盐城市盐都区九年级上学期期末考试数学试卷(解析版) 题型:选择题
如图1,在平面内选一定点O,引一条有方向的射线Ox,再选定一个单位长度,那么平面上任一点M的位置可由∠MOx的度数θ与OM的长度m确定,有序数对(θ,m)称为M点的“极坐标”,这样建立的坐标系称为“极坐标系”.在图2的极坐标系下,如果正六边形的边长为2,有一边OA在射线Ox上,则正六边形的顶点C的极坐标应记为( )
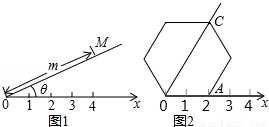
A.(60°,4) B.(45°,4) C.(60°,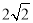 ) D.(50°,
) D.(50°,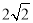 )
)
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省盐城市盐都区九年级上学期期末考试数学试卷(解析版) 题型:选择题
数据1,3,3,4,5的众数为( )
A.1 B.3 C.4 D.5
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省苏州市九年级上学期期末考试数学试卷(解析版) 题型:填空题
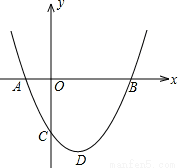
如图,二次函数y=ax2+bx+c(a>0)图象的顶点为D,其图象与x轴的交点A、B的横坐标分别为-1,3.与y轴负半轴交于点C,在下面五个结论中:
①2a-b=0;②a+b+c>0;③c=-3a;④只有当a= 时,△ABD是等腰直角三角形;⑤使△ACB为等腰三角形的a值可以有四个.
时,△ABD是等腰直角三角形;⑤使△ACB为等腰三角形的a值可以有四个.
其中正确的结论是
查看答案和解析>>
科目:初中数学 来源:2014-2015学年黑龙江省五常市九年级上学期12月阶段性测试数学试卷(解析版) 题型:选择题
一段公路的坡度为1:3,某人沿这段公路路面前进100米,那么他上升的最大高度是( )
A.30米 B.10米 C.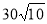 米 D.
米 D.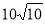 米
米
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com