
分析 利用轴对称图形的性质可作点A关于x轴的对称点A′,连接A′B,交x轴于点M,点M即为所求.
解答 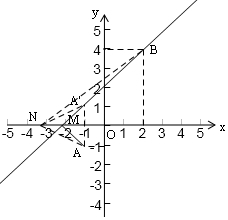 解:作点A(-1,-1)关于x轴的对称点A′(-1,1),作直线A′B交x轴于点M,
解:作点A(-1,-1)关于x轴的对称点A′(-1,1),作直线A′B交x轴于点M,
由对称性知:MA′=MA,
∴MB-MA=MB-MA′=A′B,
若N是x轴上异于M的点,则NA′=NA,这时NB-NA=NB-NA′<A′B=MB-MA′,
所以,点M就是使MB-MA的值最大的点,MB-MA的最大值是A′B,
设直线A′B的解析式为:y=kx+b,
把A′(-1,1),B(2,4)代入得:$\left\{\begin{array}{l}{-k+b=1}\\{2k+b=4}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=1}\\{b=2}\end{array}\right.$,
∴直线A′B的解析式为y=x+2,
∵点M为直线A′B与x轴的交点,
当y=0时,x+2=0,
x=-2,
∴点M的坐标为(-2,0).
故答案为:(-2,0).
点评 本题是求最值问题,考查了在直线上求作一点,使到直线两侧点的距离差最大,涉及待定系数法求一次函数的解析式及在三角形中任意两边之差小于第三边的应用,正确作出一个点的对称点是解题的关键.


 全能测控期末小状元系列答案
全能测控期末小状元系列答案科目:初中数学 来源:2016-2017学年北京市西城区七年级上学期期末考试数学试卷(解析版) 题型:单选题
甲、乙两人同时开始采摘樱桃,甲平均每小时采摘8公斤樱桃,乙平均每小时采摘7公斤樱桃。采摘同时结束后,甲从他采摘的樱桃中取出1公斤给了乙,这时两人的樱桃一样多。他们采摘樱桃用了多长时间?设他们采摘了x小时,则下面所列方程中正确的是( )
A. 8x-1=7x+1 B. 8x-1=7x C. 8x+l=7x D. 8x+l=7x-1
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 时间(秒) 路程(米) | 从比赛开始到 匀速跑前 | 从比赛开始到 匀速跑完100秒 | 从比赛开始到 匀速跑完200秒 |
| 小明 | 1600 | 1600+100a | 1600+200a |
| 小刚 | 1450 | 1450+100b | 1450+200b |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 等腰三角形 | B. | 直角三角形 | C. | 等腰直角三角形 | D. | 等边三角形 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,圆O的半径为2$\sqrt{2}$,AB、AC是圆O的两条弦,AB=2$\sqrt{3}$,AC=4,如果以O为圆心,作一个与AC相切的圆,那么这个圆的半径是多少?它与AB又怎样的位置关系?为什么?
如图,圆O的半径为2$\sqrt{2}$,AB、AC是圆O的两条弦,AB=2$\sqrt{3}$,AC=4,如果以O为圆心,作一个与AC相切的圆,那么这个圆的半径是多少?它与AB又怎样的位置关系?为什么?查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com