
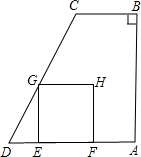
 如图,梯形ABCD中,CB∥DA,∠ABC=90°,BA=AD=4,BC=2.动点E从点D出发,以每秒1个单位的速度沿线段DA运动,到点A停止,过点E作EG⊥AD交折线D-C-B于点G,以GE为一边向右作正方形GEFH.设运动时间为t(秒),正方形GEFH与梯形ABCD重叠面积为S(平方单位).
如图,梯形ABCD中,CB∥DA,∠ABC=90°,BA=AD=4,BC=2.动点E从点D出发,以每秒1个单位的速度沿线段DA运动,到点A停止,过点E作EG⊥AD交折线D-C-B于点G,以GE为一边向右作正方形GEFH.设运动时间为t(秒),正方形GEFH与梯形ABCD重叠面积为S(平方单位).分析 (1)根据当点F与A重合时,DE+EF=AD,列式计算即可;
(2)分0<t≤$\frac{4}{3}$、$\frac{4}{3}$<t≤2和2<t≤4三种情况进行解答;
(3)分DH=DA和HD=HA,根据勾股定理列式计算即可.
解答 解:(1)当点F与A重合时,DE+EF=AD,即t+2t=4,
解得t=$\frac{4}{3}$;
(2)当0<t≤$\frac{4}{3}$时,S=2t×2t=4t2,
当$\frac{4}{3}$<t≤2时,S=2t×(4-t)=-2t2+8t,
当2<t≤4时,S=4×(4-t)=-4t+16;
(3)当DH=DA时,(3t)2+(2t)2=42,
解得t=$\frac{4\sqrt{13}}{13}$,
当HD=HA时,3t=4-3t,
解得t=$\frac{2}{3}$.
答:t=$\frac{4\sqrt{13}}{13}$或$\frac{2}{3}$时,△AHD为等腰三角形.
点评 本题考查的是直角梯形的性质、矩形面积的计算和等腰三角形的判定,灵活运用分情况讨论思想、熟练运用相关定理是解题的关键.


科目:初中数学 来源: 题型:解答题
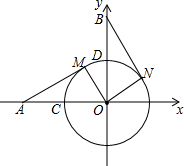 已知,如图坐标轴上点A(-4,0)、B(0,4),以点O为圆心,2为半径作⊙O与x轴的负半轴、y轴的正半轴分别交于点C、D,将扇形COD绕点O顺时针旋转α°得到扇形MON(点M与点C、点N与点D对应,其中0°≤α≤360°),连接AM、BN.
已知,如图坐标轴上点A(-4,0)、B(0,4),以点O为圆心,2为半径作⊙O与x轴的负半轴、y轴的正半轴分别交于点C、D,将扇形COD绕点O顺时针旋转α°得到扇形MON(点M与点C、点N与点D对应,其中0°≤α≤360°),连接AM、BN.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
| 球 | 两红 | 一红一白 | 两白 |
| 礼金券(元) | 5 | 10 | 5 |
| 球 | 两红 | 一红一白 | 两白 |
| 礼金券(元) | 10 | 5 | 10 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
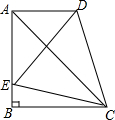 如图,在直角梯形ABCD中,AD∥BC,∠ABC=90°,AB=BC,E为AB边上一点,∠BCE=15°,且AE=AD,连接DE交AC于H.下列结论:①△ACD≌△ACE;②∠ACD=30°;③A、C两点关于DE所在直线对称;④$\frac{{S}_{△AEH}}{{S}_{△CDH}}$=$\frac{EH}{CD}$.其中正确的结论是①②.(把你认为正确的结论的序号都填上)
如图,在直角梯形ABCD中,AD∥BC,∠ABC=90°,AB=BC,E为AB边上一点,∠BCE=15°,且AE=AD,连接DE交AC于H.下列结论:①△ACD≌△ACE;②∠ACD=30°;③A、C两点关于DE所在直线对称;④$\frac{{S}_{△AEH}}{{S}_{△CDH}}$=$\frac{EH}{CD}$.其中正确的结论是①②.(把你认为正确的结论的序号都填上)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com