
【题目】已知某开发区有一块四边形的空地ABCD,如图所示,经测量∠A=90°,AB=3m,BC=12m,CD=13m,DA=4m,求这块空地的面积? 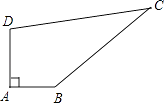
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案科目:初中数学 来源: 题型:
【题目】如图,用同样规格的黑白两色正方形瓷砖铺设矩形地面,请观察下列图形,探究并观察下列问题。
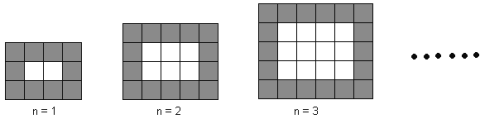
(1)在第4个图中,共有白色瓷砖 块;在第![]() 个图中,共有白色瓷砖 块;
个图中,共有白色瓷砖 块;
(2)在第4个图中,共有瓷砖 块;在第![]() 个图中,共有瓷砖 块;
个图中,共有瓷砖 块;
(3)如果每块黑瓷砖4元,白瓷砖3元,铺设当![]() 时,共需花多少钱购买瓷砖?
时,共需花多少钱购买瓷砖?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,现有一张边长为4的正方形纸片ABCD,点P为正方形AD边上的一点(不与点A、点D重合)将正方形纸片折叠,使点B落在P处,点C落在G处,PG交DC于H,折痕为EF,连接BP、BH. 
(1)求证:∠APB=∠BPH;
(2)当点P在边AD上移动时,△PDH的周长是否发生变化?并证明你的结论;
(3)设AP为x,四边形EFGP的面积为S,求出S与x的函数关系式,试问S是否存在最小值?若存在,求出这个最小值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两地距离300km,一辆货车和一辆轿车先后从甲地出发驶向乙地.如图,线段OA表示货车离甲地的距离y(km)与时间x(h)之间的函数关系,折线BCDE表示轿车离甲地的距离y(km)与时间x(h)之间的函数关系,根据图像,解答下列问题: 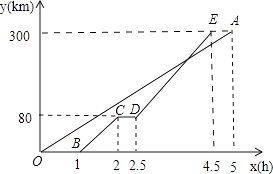
(1)线段CD表示轿车在中途停留了h;
(2)求轿车从甲地出发后经过多长时间追上货车.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】A、B两种机器人都被用来搬运化工原料,A型机器人比B型机器人每小时多搬运20千克,A型机器人搬运1000千克所用时间与B型机器人搬运800千克所用时间相等,两种机器人每小时分别搬运多少化工原料?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】请根据图中提供的信息,回答下列问题:
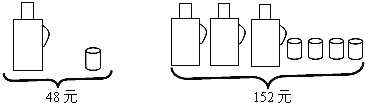
一个水瓶与一个水杯分别是多少元?
(2)甲、乙两家商场同时出售同样的水瓶和水杯,为了迎接新年,两家商场都在搞促销活动,甲商场规定:这两种商品都打八折;乙商场规定:买一个水瓶赠送两个水杯,另外购买的水杯按原价卖.若某单位想要买5个水瓶和20个水杯,请问选择哪家商场购买更合算,并说明理由.(必须在同一家购买)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】A、B两厂在公路的同侧,现欲在公路边建一货场C.
(1)若要使货场到两厂的距离相等,请在图1中作出此时货场的位置.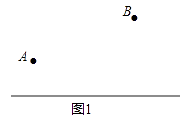
(2)若要求所修公路(即A、B两厂到货场的距离之和)最短,请在图2中作出货场的位置.(用尺规作图,保留作图痕迹,不必写作法)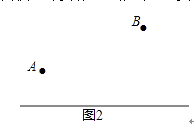
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在弹簧限度内,弹簧挂上物体后弹簧的长度与所挂物体的质量之间的关系如下表:
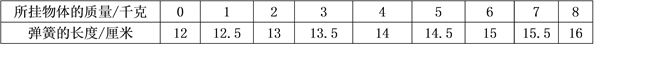
(1)上表中,自变量是 ,因变量是 ;
(2)弹簧不挂物体的长度是 ;
(3)如果用x表示弹性限度内物体的质量,用y表示弹簧的长度,那么随着x的变化,y的变化趋势是 ,写出y与x的关系式 ;
(4)如果弹簧最大挂质量为25千克,你能计算出当挂重为14千克时,弹簧的长度是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com