

分析 (1)该圆与数轴重合的点所表示的数,就是大圆的周长;
(2)①分别计算出第几次滚动后,小圆离原点的距离,比较作答;
②先计算总路程,因为大圆不动,计算各数之和为-10,即小圆最后的落点为原点左侧,向左滚动10秒,距离为10π;
(3)分四种情况进行讨论:大圆和小圆分别在同侧,异侧时,表示出各自与数轴重合的点所表示的数.根据两圆与数轴重合的点之间相距6π列等式,求出即可.
解答 解:(1)若大圆沿数轴向左滚动1周,则该圆与数轴重合的点所表示的数是-2π•2=-4π,
故答案为:-4π;
(2)①第1次滚动后,|-1|=1,
第2次滚动后,|-1+2|=1,
第3次滚动后,|-1+2-4|=3,
第4次滚动后,|-1+2-4-2|=5,
第5次滚动后,|-1+2-4-2+3|=2,
第6次滚动后,|-1+2-4-2+3-8|=10,
则第6次滚动后,小圆离原点最远;
②1+2+4+3+2+8=20,
20×π=20π,
-1+2-4-2+3-8=-10,
∴当小圆结束运动时,小圆运动的路程共有20π,此时两圆与数轴重合的点之间的距离是10π;
(3)设时间为t秒,
分四种情况讨论:
i)当两圆同向右滚动,
由题意得:t秒时,大圆与数轴重合的点所表示的数:2πt,
小圆与数轴重合的点所表示的数为:πt,
2πt-πt=6π,
2t-t=6,
t=6,
2πt=12π,πt=6π,
则此时两圆与数轴重合的点所表示的数分别为12π、6π.
ii)当两圆同向左滚动,
由题意得:t秒时,大圆与数轴重合的点所表示的数:-2πt,
小圆与数轴重合的点所表示的数:-πt,
-πt+2πt=6π,
-t+2t=6,
t=6,
-2πt=-12π,-πt=-6π,
则此时两圆与数轴重合的点所表示的数分别为-12π、-6π.
iii)当大圆向右滚动,小圆向左滚动时,
同理得:2πt-(-πt)=6π,
3t=6,
t=2,
2πt=4π,-πt=-2π,
则此时两圆与数轴重合的点所表示的数分别为4π、-2π.
iiii)当大圆向左滚动,小圆向右滚动时,
同理得:πt-(-2πt)=6π,
t=2,
πt=2π,-2πt=-4π,
则此时两圆与数轴重合的点所表示的数分别为-4π、2π.
点评 本题考查了数轴及圆的几何变换,还考查了一元一次方程的应用,用方程解决此类问题比较简单,同时又利用了分类讨论的思想,明确向右移动坐标加的关系,向左移动坐标减的关系.


科目:初中数学 来源: 题型:解答题
 某城市采用分段计费的方法来计算电费,月用电量x度与相应电费y元之间的函数关系如图:
某城市采用分段计费的方法来计算电费,月用电量x度与相应电费y元之间的函数关系如图:查看答案和解析>>
科目:初中数学 来源:2017届江苏省扬州市九年级下学期第一次月考数学试卷(解析版) 题型:解答题
为了解八年级学生的课外阅读情况,学校从八年级随机抽取了若干名学生,对他们的读书时间进行了调查并将收集的数据绘成了两幅不完整的统计图,请你依据图中提供的信息,解答下列问题:(说明:每组时间段含最小值不含最大值)

(1)从八年级抽取了多少名学生?
(2)①“2 ? 2.5小时”的部分对应的扇形圆心角为 度;
②课外阅读时间的中位数落在 内.(填时间段)
(3)如果八年级共有800名学生,请估算八年级学生课外阅读时间不少于1.5小时的有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{{x}^{2}}$=($\sqrt{x}$)2 | B. | $\root{3}{{x}^{3}}$=$\sqrt{{x}^{2}}$ | C. | $\sqrt{{(-x)}^{2}}$=|-x| | D. | $\sqrt{{x}^{2}-4}$=$\sqrt{x+2}$•$\sqrt{x-2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
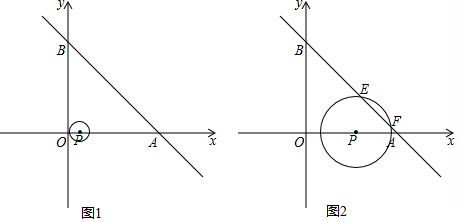
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
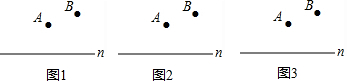
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com