练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    19．一个扇形的圆心角为100°，面积为15π cm2，则此扇形的半径长为3$\sqrt{6}$cm．

    分析 根据扇形的面积公式S=$\frac{nπ{R}^{2}}{360}$即可求得半径．

    解答 解：设该扇形的半径为R，则$\frac{100π×{R}^{2}}{360}$=15π，
    解得R=3$\sqrt{6}$．
    即该扇形的半径为3$\sqrt{6}$cm．
    故答案是：3$\sqrt{6}$cm．

    点评 本题考查了扇形面积的计算．正确理解公式是关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：选择题

    9．下列运算正确的是（　　）
    A．x2+x2=x4B．x2•x3=x6C．（-2x3）2=-4x6D．（x3）2=x6

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    10．雾霾天气给人们的健康带来严重危害．教生物的李老师通过显微镜，将空气中细小的霾颗粒放大1000倍，发现这些霾颗粒平均直径为15微米〜25微米，其中25微米（1微米=0.000001米）用科学记数法可表示为（　　）
    A．2.5×106B．2.5×105C．2.5×10-5D．2.5×10-6

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    7．某单位750名职工积极参加向贫困地区学校捐书活动，为了解职工的捐书量，采用随机抽样的方法抽取30名职工作为样本，对他们的捐书量进行统计，统计结果共有4本、5本、6本、7本、8本五类，分别用A、B、C、D、E表示，根据统计数据绘制成了如图所示的不完整的条形统计图，由图中给出的信息解答下列问题：
    （1）补全条形统计图；
    （2）求这30名职工捐书本数的平均数、众数和中位数；
    （3）估计该单位750名职工共捐书多少本？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

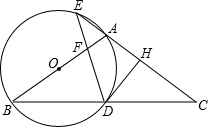    14．如图，在△ABC中，AB=AC，以AB为直径作圆O，分别交BC于点D，交CA的延长线于点E，过点D作DH⊥AC于点H，连接DE交线段OA于点F．
    （1）求证：DH是圆O的切线；
    （2）若A为EH的中点，求$\frac{EF}{FD}$的值；
    （3）若EA=EF=1，求圆O的半径．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    4．为了解某市老人的身体健康状况，需要抽取部分老人进行调查，下列抽取老人的方法最合适的是（　　）
    A．随机抽取100位女性老人
    B．随机抽取100位男性老人
    C．随机抽取公园内100位老人
    D．在城市和乡镇各选10个点，每个点任选5位老人

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    11．如图，将直尺与含30°角的三角尺摆放在一起，若∠1=20°，则∠2的度数是（　　）
    A．50°B．60°C．70°D．80°

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

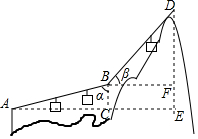    8．如图，游客在点A处坐缆车出发，沿A-B-D的路线可至山顶D处，假设AB和BD都是直线段，且AB=BD=600m，α=75°，β=45°，求DE的长．
    （参考数据：sin75°≈0.97，cos75°≈0.26，$\sqrt{2}$≈1.41）

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    20．如图所示，已知EF⊥AB，垂足为F，CD⊥AB，垂足为D，∠1=∠2，试判断∠AGD和∠ACB是否相等，为什么？（将解答过程补充完整）
    解：∠AGD=∠ACB．
    理由如下：EF⊥AB，CD⊥AB（已知）
    ∴∠EFB=∠CDB=90° （垂直的定义）
    ∴CD∥EF （垂直于同一条直线的两条直线互相平行）
    ∴∠1=∠ECD（两直线平行，同位角相等）
    又∠1=∠2（已知）
    ∴∠ECD=∠2（  等量代换 ）
    ∴DG∥BC （ 内错角相等，两直线平行 ）
    ∴∠AGD=∠ACB （两直线平行，同位角相等）．

    查看答案和解析>>

    同步练习册答案