
����Ŀ����֪������x�Ķ��κ���y��ax2��2ax��a��0���Ķ���ΪC����x�ύ�ڵ�O��A������x��һ�κ���y����ax��a��0����
��1����˵����C��һ�κ�����ͼ���ϣ�
��2���������㣨k��y1������k+2��y2����k��0����2�����ڶ��κ�����ͼ���ϣ��Ƿ��������k������![]() ��������ڣ������k��ֵ����������ڣ���˵�����ɣ�
��������ڣ������k��ֵ����������ڣ���˵�����ɣ�
��3������E�Ƕ��κ���ͼ����һ���㣬E��ĺ�������n���ҩ�1��n��1������E��y���ƽ���ߣ���һ�κ���ͼ���ڵ�F����0��a��2ʱ�����߶�EF�����ֵ��
���𰸡�(1)����������2�����ڣ�����k��ֵΪ��4����3��EF�����ֵ��4��
��������
��1����������κ���y��ax2��2ax��a��x��1��2��a����C��1����a������x��1ʱ��һ�κ���ֵy����a���Ե�C��һ�κ���y����ax��ͼ���ϣ�
��2�����ڣ����㣨k��y1������k+2��y2����k��0����2��������κ�������ʽ����a��k��ʾ��y1��y2����Ϊ����![]() ,��y1��y2���������ɵù���k�ķ��̣��ⷽ�̼��鼴�����k��ֵ.
,��y1��y2���������ɵù���k�ķ��̣��ⷽ�̼��鼴�����k��ֵ.
��3��������������ۣ��ٵ���1��n��0ʱ��EF��yE��yF��an2��2an������an����![]() �ڵ�0��n��1ʱ��EF��yF��yE����an����an2��2an����
�ڵ�0��n��1ʱ��EF��yF��yE����an����an2��2an����![]()
��1���߶��κ���y��ax2��2ax��a��x��1��2��a��
�ඥ��C��1����a����
�ߵ�x��1ʱ��һ�κ���ֵy����a
���C��һ�κ���y����ax��ͼ���ϣ�
��2�����ڣ�
�ߵ㣨k��y1������k+2��y2����k��0����2�����ڶ��κ�����ͼ���ϣ�
��y1��ak2��2ak��y2��a��k+2��2��2a��k+2����
������![]()
��![]() ��
��
�������� ![]() ��
��
��![]()
��![]() ��
��
���k����4��
�����飺k����4��ԭ���̵ĸ���
������k��ֵΪ��4��
��3���ߵ�E�Ƕ��κ���ͼ����һ���㣬
��E��n��an2��2an����
��EF��y�ᣬF��һ�κ���ͼ���ϣ���F��n����an����
�ٵ���1��n��0ʱ��EF��yE��yF��an2��2an������an����![]()
��a��0��
�൱n����1ʱ��EF�����ֵ�������ֵ��2a��
�֡�0��a��2��
��0��2a��4����EF�����ֵ��4��
�ڵ�0��n��1ʱ��EF��yF��yE����an����an2��2an����![]() ��ʱEF�����ֵ��
��ʱEF�����ֵ��![]() ��
��
�֡�0��a��2��
��0��![]() ��
��![]() ����EF�����ֵ��
����EF�����ֵ��![]() ��
��
����������EF�����ֵ��4��


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����A�Ƿ���������y��![]() ͼ����һ�㣬����A��x���ƽ���߽�����������y����
ͼ����һ�㣬����A��x���ƽ���߽�����������y����![]() ��ͼ���ڵ�B����C��x���ϣ���S��ABC��
��ͼ���ڵ�B����C��x���ϣ���S��ABC��![]() ����k=��������
����k=��������
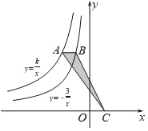
A. 6B. ��6C. ![]() D. ��
D. ��![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ��չѧ���ĺ�������������ѧ�����ۺ�������ijѧУ�ƻ���������ѡ�Σ��������赸���滭���鷨��ѧУ��ȡ��������ķ��������ʾ�����![]() ÿ���������ѧ������ѡ�����ֻ��ѡ������һ��
ÿ���������ѧ������ѡ�����ֻ��ѡ������һ��![]() �Ե������������������Ƴ�����������������ͳ��ͼ
�Ե������������������Ƴ�����������������ͳ��ͼ![]() ����ͼ��������Ϣ����������⣺
����ͼ��������Ϣ����������⣺


![]() ���ε����ѧ������______�ˣ�������ͳ��ͼ�У�m��ֵ��______��
���ε����ѧ������______�ˣ�������ͳ��ͼ�У�m��ֵ��______��
![]() �ֱ�����μӵ����ѧ����ѡ��滭���鷨����������������ͳ��ͼ����������
�ֱ�����μӵ����ѧ����ѡ��滭���鷨����������������ͳ��ͼ����������
![]() ��У����ѧ��2000�ˣ����Ƹ�УԼ�ж�����ѡ�������γ̣�
��У����ѧ��2000�ˣ����Ƹ�УԼ�ж�����ѡ�������γ̣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ͼ����![]() �У�
�У�![]() ����D��E�ֱ���AB��AC���е㣬��F��BC�ӳ����ϣ�����EF����
����D��E�ֱ���AB��AC���е㣬��F��BC�ӳ����ϣ�����EF����![]() ��
��
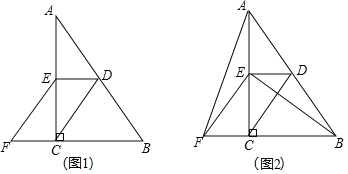
![]() ��ͼ1����֤���ı���CDEF��ƽ���ı��Σ�
��ͼ1����֤���ı���CDEF��ƽ���ı��Σ�
![]() ��ͼ2������AF��BE���ڲ������κθ����ߵ�����£���ֱ��д��ͼ2��������
��ͼ2������AF��BE���ڲ������κθ����ߵ�����£���ֱ��д��ͼ2��������![]() �����ȵ������Σ�
�����ȵ������Σ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
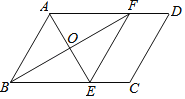
����Ŀ����֪����ͼ����ƽ���ı���ABCD�У���BAD��ƽ���߽�BC�ڵ�E����ABC��ƽ���߽�AD�ڵ�F��
��1����֤���ı���ABEF�����Σ�
��2����AE��6��BF��8��ƽ���ı���ABCD�������36����AD�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ABC�У���ACB��90�㣮С��ͬѧ����ֱ�ߺ�Բ�������������ͼ��
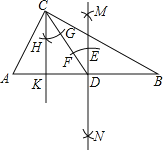
�ٷֱ��Ե�A��BΪԲ�ģ��Դ���![]() AB��Ϊ�뾶�������������ڵ�M��N������M��N��ֱ����AB���ڵ�D��
AB��Ϊ�뾶�������������ڵ�M��N������M��N��ֱ����AB���ڵ�D��
������CD���Ե�DΪԲ�ģ���һ����Ϊ�뾶��������MN�ڵ�E����CD�ڵ�F���Ե�CΪԲ�ģ���ͬ������Ϊ�뾶��������CD���ڵ�G���Ե�GΪԲ�ģ���EF��Ϊ�뾶������ǰ�����ڵ�H��������CH��AB���ڵ�K����������ϲ����������������
��1���ɳ߹���ͼ��֪��ֱ��MN���߶�AB���� ���ߣ���DCK���� ����
��2����CD��5��AK��2����CK�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ֱ��l1��y1��![]() x��l2��y2��
x��l2��y2��![]() x��l3��y3����
x��l3��y3����![]() x��l4��y4����
x��l4��y4����![]() x��OA1��1������A1��A1A2��x�ύl1�ڵ�A2���ٹ���A2��A2A3��l1����l2�ڵ�A3���ٹ���A3��A3A4��l2��y���ڵ�A4�����������A2020������Ϊ_____��
x��OA1��1������A1��A1A2��x�ύl1�ڵ�A2���ٹ���A2��A2A3��l1����l2�ڵ�A3���ٹ���A3��A3A4��l2��y���ڵ�A4�����������A2020������Ϊ_____��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һ����ѧ�ۺ�ʵ����У�С���ƻ��������Ŵ�¥�ĸ߶ȣ��ڵ�B�����¥��A������Ϊ22�����������ų�¥ǰ��21����C�����ٵ���3�ߵ�¥̨D��������ô�ʱ¥��A������Ϊ45����
��1������Ŵ�¥�ĸ߶ȣ�
��2��ÿ���ش���գ����Ŵ�¥��������Ҫ��A��B֮���������ӣ����������Ϲ�һЩ���죬�������A��B֮�����Ҳ���ij��ȣ�������������������ο����ݣ�sin22���![]() ��cos22���
��cos22���![]() ��tan22���
��tan22���![]() ��
��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
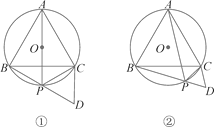
����Ŀ����ͼ���ȱ�������ABC�Ķ����ڡ�O�ϣ���P���ӻ�![]() �ϵ�һ��(�˵����)���ӳ�BP����D��ʹBD��AP������CD.
�ϵ�һ��(�˵����)���ӳ�BP����D��ʹBD��AP������CD.
(1)��AP��Բ��O����ͼ�٣������жϡ�PDC��ʲô�����Σ���˵�����ɣ�
(2)��AP����Բ��O����ͼ�ڣ���PDC����ʲô�����Σ�Ϊʲô��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com