
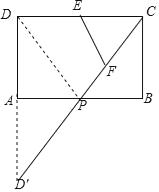
【题目】如图,矩形△ABCD中,AB=2,AD=1,E为CD中点,P为AB边上一动点(含端点),F为CP中点,则△CEF的周长最小值为_____.

【答案】![]() +1.
+1.
【解析】
根据三角形的中位线的性质得到EF=![]() PD,得到C△CEF=CE+CF+EF=CE+
PD,得到C△CEF=CE+CF+EF=CE+![]() (CP+PD)=
(CP+PD)=![]() (CD+PC+PD)=
(CD+PC+PD)=![]() C△CDP,当△CDP的周长最小时,△CEF的周长最小;即PC+PD的值最小时,△CEF的周长最小;如图,作D关于AB的对称点D′,连接CD′交AB于P,于是得到结论.
C△CDP,当△CDP的周长最小时,△CEF的周长最小;即PC+PD的值最小时,△CEF的周长最小;如图,作D关于AB的对称点D′,连接CD′交AB于P,于是得到结论.
解:∵E为CD中点,F为CP中点,
∴EF=![]() PD,
PD,
∴C△CEF=CE+CF+EF=CE+![]() (CP+PD)=
(CP+PD)=![]() (CD+PC+PD)=
(CD+PC+PD)=![]() C△CDP,
C△CDP,
∴当△CDP的周长最小时,△CEF的周长最小;
即PC+PD的值最小时,△CEF的周长最小;
如图,作D关于AB的对称点D′,连接CD′交AB于P,
∵AD=AD′=BC,AD′∥BC,
∴四边形AD′BC是平行四边形,
∴AP=PB=1,PD′=PC,
∴CP=PD=![]() ,
,
∴C△CEF=![]() C△CDP=
C△CDP=![]() +1,
+1,
故答案为:![]() +1.
+1.


 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案科目:初中数学 来源: 题型:
【题目】如图1,平面直角坐标系中,抛物线y=ax2+bx+3与x轴的两个交点分别为A(﹣3,0),B(1,0),与y轴的交点为D,对称轴与抛物线交于点C,与x轴负半轴交于点H.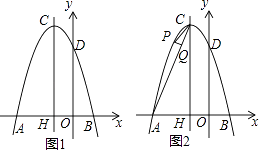
(1)求抛物线的表达式;
(2)点E,F分别是抛物线对称轴CH上的两个动点(点E在点F上方),且EF=1,求使四边形BDEF的周长最小时的点E,F坐标及最小值;
(3)如图2,点P为对称轴左侧,x轴上方的抛物线上的点,PQ⊥AC于点Q,是否存在这样的点P使△PCQ与△ACH相似?若存在请求出点P的坐标,若不存在请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
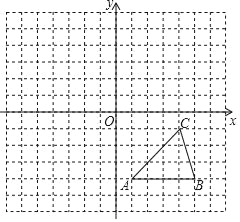
【题目】如图,在平面直角坐标系中,△ABC三个顶点的坐标分别为:A(1,﹣4),B(5,﹣4),C(4,﹣1).
(1)将△ABC经过平移得到△A1B1C1,若点C的应点C1的坐标为(2,5),写出点A,B的对应点A1,B1的坐标;
(2)在如图的坐标系中画出△A1B1C1,并画出与△A1B1C1关于原点O成中心对称的△A2B2C2.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】点A、B在数轴上表示的数如图所示,动点P从点A出发,沿数轴向右以每秒1个单位长度的速度向点B运动到点B停止运动;同时,动点Q从点B出发,沿数轴向左以每秒2个单位长度的速度向点A运动,到点A停止运动设点P运动的时间为t秒,P、Q两点的距离为d(d≥0)个单位长度.
(1)当t=1时,d= ;
(2)当P、Q两点中有一个点恰好运动到线段AB的中点时,求d的值;
(3)当点P运动到线段AB的3等分点时,直接写出d的值;
(4)当d=5时,直接写出t的值.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】教室里的饮水机接通电源就进入自动程序,开机加热时每分钟上升10℃,加热到100℃,停止加热,水温开始下降,此时水温(℃)与开机后用时(min)成反比例关系.直至水温降至30℃,饮水机关机.饮水机关机后即刻自动开机,重复上述自动程序.若在水温为30℃时,接通电源后,水温y(℃)和时间(min)的关系如图,为了在上午第一节下课时(8:45)能喝到不超过50℃的水,则接通电源的时间可以是当天上午的( )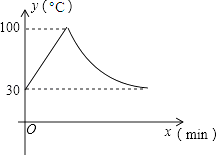
A.7:20
B.7:30
C.7:45
D.7:50
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形OABC是矩形,ADEF是正方形,点A、D在x轴的正半轴上,点C在y轴的正半轴上,点F在AB上,点B、E在反比例函数y= ![]() 的图象上,OA=1,OC=6,则正方形ADEF的边长为 .
的图象上,OA=1,OC=6,则正方形ADEF的边长为 . 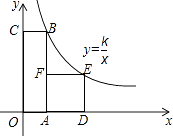
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一次函数y=(k﹣2)x﹣3k2+12.
(1)k为何值时,图象经过原点;
(2)k为何值时,图象与直线y=﹣2x+9的交点在y轴上;
(3)k为何值时,图象平行于y=﹣2x的图象;
(4)k为何值时,y随x增大而减小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠A=60°,BD、CD分别平分∠ABC、∠ACB,M、N、Q分别在DB、DC、BC的延长线上,BE、CE分别平分∠MBC、∠BCN,BF、CF分别平分∠EBC、∠ECQ,则∠F=________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠BAC=40°,∠ACB=60°,D为△ABC外一点,DA平分∠BAC,且CBD=50°,则∠DCB的度数是_______.
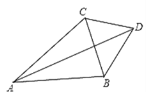
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com