
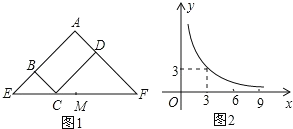
【题目】图1所示矩形ABCD中,BC=x,CD=y,y与x满足的反比例函数关系如图2所示,等腰直角三角形AEF的斜边EF过C点,M为EF的中点,则下列结论正确的序号是___.①当x=3时,EC<EM;②当y=9时,EC>EM③当x增大时,ECCF的值增大;④当y增大时,BEDF的值不变。
【答案】④
【解析】
由于等腰直角三角形AEF的斜边EF过C点,则△BEC和△DCF都是直角三角形;观察反比例函数图象得反比例解析式为y=![]() ;当x=3时,y=3,即BC=CD=3,根据等腰直角三角形的性质得CE=3
;当x=3时,y=3,即BC=CD=3,根据等腰直角三角形的性质得CE=3![]() ,CF=3
,CF=3![]() ,则C点与M点重合;当y=9时,根据反比例函数的解析式得x=1,即BC=1,CD=9,所以EF=10
,则C点与M点重合;当y=9时,根据反比例函数的解析式得x=1,即BC=1,CD=9,所以EF=10![]() ,而EM=5
,而EM=5![]() ;由于ECCF=
;由于ECCF=![]() x×
x×![]() y;利用等腰直角三角形的性质BEDF=BCCD=xy,然后再根据反比例函数的性质得BEDF=9,其值为定值.
y;利用等腰直角三角形的性质BEDF=BCCD=xy,然后再根据反比例函数的性质得BEDF=9,其值为定值.
因为等腰直角三角形AEF的斜边EF过C点,M为EF的中点,所以△BEC和△DCF都是直角三角形;
观察反比例函数图象得x=3,y=3,则反比例解析式为y=![]() ;
;
①、当x=3时,y=3,即BC=CD=3,所以CE=![]() BC=3
BC=3![]() ,CF=
,CF=![]() CD=3
CD=3![]() ,C点与M点重合,则EC=EM,所以①错误;
,C点与M点重合,则EC=EM,所以①错误;
②、当y=9时,x=1,即BC=1,CD=9,所以EC=![]() ,EF=10
,EF=10![]() ,EM=5
,EM=5![]() ,所以②错误;
,所以②错误;
③、因为ECCF=![]() x
x![]() y=2×xy=18,所以,ECCF为定值,所以③错误;
y=2×xy=18,所以,ECCF为定值,所以③错误;
④、因为BEDF=BCCD=xy=9,即BEDF的值不变,所以④正确.
故答案为:④.


科目:初中数学 来源: 题型:
【题目】如图,□ABCD中,AB=6,E是BC边的中点,F为CD边上一点,DF=4.8,∠DFA=2∠BAE,则AF 的长为( )
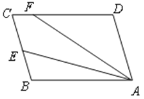
A. 4.8B. 6C. 7.2D. 10.8
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两家商场都以m(m>1000)元的价格购进了10台电器,每台销售定价都为n元.但在实际销售中,各自推出了优惠方案,甲商场规定:凡超过1000元的电器,超出的金额按90%收取;乙商场规定:凡超过500元的电器,超出的金额按95%收取.一段时间后,两家商场各自销售完了这10台电器,并且都有了盈利.
(1)如果销售完这10台电器,两家商场的盈利各多少元(结果用含m,n的式子表示)?
(2)如果销售完这10台电器,两家商场的盈利相差多少元(结果用含m,n的式子表示)?
(3)如果n=1700,那么某顾客想购买该种电器,应选择哪一家商场购买比较合算?说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明家的洗手盆上装有一种抬启式水龙头(如图1),完全开启后,水流路线呈抛物线,把手端点A,出水口B和落水点C恰好在同一直线上,点A至出水管BD的距离为12cm,洗手盆及水龙头的相关数据如图2所示,现用高10.2cm的圆柱型水杯去接水,若水流所在抛物线经过点D和杯子上底面中心E,则点E到洗手盆内侧的距离EH为_________cm.
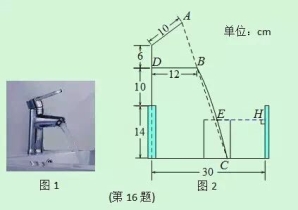
(第16题图)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若用点A,B,C分别表示有理数a,b,c,它们在数轴上的位置如图所示.
![]()
(1)比较a,b,c的大小(用“<”连接);
(2)请在横线上填上>,< 或 =:a+b____ 0 , b-c____ 0;
(3)化简:2c+|a+b|+|c-b|-|c-a|.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两同学的家与学校的距离均为3000米.甲同学先步行600米,然后乘公交车去学校、乙同学骑自行车去学校.已知甲步行速度是乙骑自行车速度的![]() ,公交车的速度是乙骑自行车速度的2倍.甲乙两同学同时从家发去学校,结果甲同学比乙同学早到2分钟.
,公交车的速度是乙骑自行车速度的2倍.甲乙两同学同时从家发去学校,结果甲同学比乙同学早到2分钟.
(1)求乙骑自行车的速度;
(2)当甲到达学校时,乙同学离学校还有多远?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某一公路的道路维修工程,准备从甲、乙两个工程队选一个队单独完成,根据两队每天的工程费用和每天完成的工程量可知,若由两队合做6天可以完成,共需工程费用385200元;若单独完成,甲队比乙队少用5天,每天的工程费用甲队比乙队多4000元。
(1)求甲、乙独做各需多少天?
(2)若从节省资金的角度,应该选择哪个工程队?
查看答案和解析>>
科目:初中数学 来源: 题型:
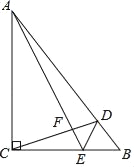
【题目】如图,△ABC,∠ACB=90°,点D,E分别在AB,BC上,AC=AD,∠CDE=45°,CD与AE交于点F,若∠AEC=∠DEB,CE=![]() ,则CF=______.
,则CF=______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com