
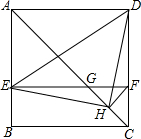
 如图,在正方形ABCD中,AC为对角线,E为AB上一点,过点E作EF∥AD,与AC、DC分别交于点G,F,H为CG的中点,连接DE,EH,DH,FH.下列结论:
如图,在正方形ABCD中,AC为对角线,E为AB上一点,过点E作EF∥AD,与AC、DC分别交于点G,F,H为CG的中点,连接DE,EH,DH,FH.下列结论:分析 ①根据题意可知∠ACD=45°,则GF=FC,则EG=EF-GF=CD-FC=DF;
②由SAS证明△EHF≌△DHC,得到∠HEF=∠HDC,从而∠AEH+∠ADH=∠AEF+∠HEF+∠ADF-∠HDC=180°;
③同②证明△EHF≌△DHC即可;
④若$\frac{AE}{AB}$=$\frac{2}{3}$,则AE=2BE,可以证明△EGH≌△DFH,则∠EHG=∠DHF且EH=DH,则∠DHE=90°,△EHD为等腰直角三角形,过H点作HM垂直于CD于M点,设HM=x,则DM=5x,DH=$\sqrt{26}$x,CD=6x,则S△DHC=$\frac{1}{2}$×HM×CD=3x2,S△EDH=$\frac{1}{2}$×DH2=13x2.
解答 解:①∵四边形ABCD为正方形,EF∥AD,
∴EF=AD=CD,∠ACD=45°,∠GFC=90°,
∴△CFG为等腰直角三角形,
∴GF=FC,
∵EG=EF-GF,DF=CD-FC,
∴EG=DF,故①正确;
②∵△CFG为等腰直角三角形,H为CG的中点,
∴FH=CH,∠GFH=$\frac{1}{2}$∠GFC=45°=∠HCD,
在△EHF和△DHC中,$\left\{\begin{array}{l}{EF=CD}\\{∠EFH=∠DCH}\\{FH=CH}\end{array}\right.$,
∴△EHF≌△DHC(SAS),
∴∠HEF=∠HDC,
∴∠AEH+∠ADH=∠AEF+∠HEF+∠ADF-∠HDC=∠AEF+∠ADF=180°,故②正确;
③∵△CFG为等腰直角三角形,H为CG的中点,
∴FH=CH,∠GFH=$\frac{1}{2}$∠GFC=45°=∠HCD,
在△EHF和△DHC中,$\left\{\begin{array}{l}{EF=CD}\\{∠EFH=∠DCH}\\{FH=CH}\end{array}\right.$,
∴△EHF≌△DHC(SAS),故③正确;
④∵$\frac{AE}{AB}$=$\frac{2}{3}$,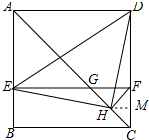
∴AE=2BE,
∵△CFG为等腰直角三角形,H为CG的中点,
∴FH=GH,∠FHG=90°,
∵∠EGH=∠FHG+∠HFG=90°+∠HFG=∠HFD,
在△EGH和△DFH中,$\left\{\begin{array}{l}{ED=DF}\\{∠EGH=∠HFD}\\{GH=FH}\end{array}\right.$,
∴△EGH≌△DFH(SAS),
∴∠EHG=∠DHF,EH=DH,∠DHE=∠EHG+∠DHG=∠DHF+∠DHG=∠FHG=90°,
∴△EHD为等腰直角三角形,
过H点作HM垂直于CD于M点,如图所示:
设HM=x,则DM=5x,DH=$\sqrt{26}$x,CD=6x,
则S△DHC=$\frac{1}{2}$×HM×CD=3x2,S△EDH=$\frac{1}{2}$×DH2=13x2,
∴3S△EDH=13S△DHC,故④正确;
故答案为:①②③④.
点评 本题考查了正方形的性质、全等三角形的判定与性质、等腰直角三角形的判定与性质、勾股定理、三角形面积的计算等知识;熟练掌握正方形的性质,证明三角形全等是解决问题的关键.


 目标测试系列答案
目标测试系列答案科目:初中数学 来源: 题型:选择题
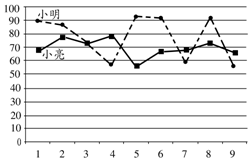 小明和小亮组成团队参加某科学比赛.该比赛的规则是:每轮比赛一名选手参加,若第一轮比赛得分满60则另一名选手晋级第二轮,第二轮比赛得分最高的选手所在团队取得胜利.为了在比赛中取得更好的成绩,两人在赛前分别作了九次测试,如图为二人测试成绩折线统计图,下列说法合理的是( )
小明和小亮组成团队参加某科学比赛.该比赛的规则是:每轮比赛一名选手参加,若第一轮比赛得分满60则另一名选手晋级第二轮,第二轮比赛得分最高的选手所在团队取得胜利.为了在比赛中取得更好的成绩,两人在赛前分别作了九次测试,如图为二人测试成绩折线统计图,下列说法合理的是( )| A. | ①③ | B. | ①④ | C. | ②③ | D. | ②④ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (a+2)2=a2+4 | B. | x3+x2=x5 | C. | $\frac{2}{2x+y}$=$\frac{1}{x+y}$ | D. | (-3a3)2=9a6 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
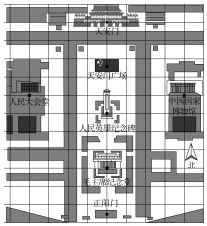 如图,是利用平面直角坐标系画出的天安门广场的平面示意图,若这个坐标系分别以正东、正北方向为x轴、y轴的正方向,表示国旗杆的点的坐标为(0,2.5),表示中国国家博物馆的点的坐标为(4,1),则表示下列建筑的点的坐标正确的是( )
如图,是利用平面直角坐标系画出的天安门广场的平面示意图,若这个坐标系分别以正东、正北方向为x轴、y轴的正方向,表示国旗杆的点的坐标为(0,2.5),表示中国国家博物馆的点的坐标为(4,1),则表示下列建筑的点的坐标正确的是( )| A. | 天安门(0,4) | B. | 人民大会堂(-4,1) | ||
| C. | 毛主席纪念堂(-1,-3) | D. | 正阳门(0,-5) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com