
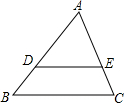 如图,已知D为△ABC边AB上一点,AD=2BD,DE∥BC交AC于E,AE=6,则EC=3.
如图,已知D为△ABC边AB上一点,AD=2BD,DE∥BC交AC于E,AE=6,则EC=3.  举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 已知点A在反比例函数y=$\frac{3}{x}$的图象上,点B与点A关于原地对称,BC∥y轴,与反比例函数y=-$\frac{2}{x}$的图象交于点C,连接AC,则△ABC的面积为5.
已知点A在反比例函数y=$\frac{3}{x}$的图象上,点B与点A关于原地对称,BC∥y轴,与反比例函数y=-$\frac{2}{x}$的图象交于点C,连接AC,则△ABC的面积为5.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 小明到工厂参加社会实践活动时,发现工人师傅测量一块木板两边AB与CD是否平行时,将直角尺(∠MFN=90°)如图放置:MF交AB于点E,NF交CD于点G,测得∠1=140°,∠2=50°.小明马上用所学数学知识帮师傅进行了证明.请你写出规范的证明过程.
小明到工厂参加社会实践活动时,发现工人师傅测量一块木板两边AB与CD是否平行时,将直角尺(∠MFN=90°)如图放置:MF交AB于点E,NF交CD于点G,测得∠1=140°,∠2=50°.小明马上用所学数学知识帮师傅进行了证明.请你写出规范的证明过程.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 问题:如图,BD是∠ABC的平分线,ED∥BC,且∠FED=∠BDE.
问题:如图,BD是∠ABC的平分线,ED∥BC,且∠FED=∠BDE.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com