
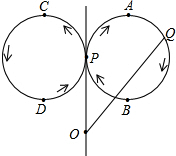
 如右图所示,点Q表示蜜蜂,它从点P出发,按照着箭头所示的方向沿P→A→B→P→C→D→P的路径匀速飞行,此飞行路径是一个以直线l为对称轴的轴对称图形,在直线l上的点O处(点O与点P不重合)利用仪器测量了∠POQ的大小.设蜜蜂飞行时间为x,∠POQ的大小为y,则下列图象中,能表示y与x的函数关系的图象大致是( )
如右图所示,点Q表示蜜蜂,它从点P出发,按照着箭头所示的方向沿P→A→B→P→C→D→P的路径匀速飞行,此飞行路径是一个以直线l为对称轴的轴对称图形,在直线l上的点O处(点O与点P不重合)利用仪器测量了∠POQ的大小.设蜜蜂飞行时间为x,∠POQ的大小为y,则下列图象中,能表示y与x的函数关系的图象大致是( )| A. | 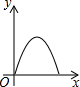 | B. | 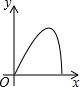 | C. | 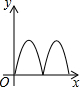 | D. | 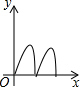 |
分析 先分析∠POQ的增减情况,再确定∠POQ增大的过程用的时间要大于∠POQ减小的过程用的时间即可得出答案.
解答 解:∵蜜蜂按照着箭头所示的方向沿P→A→B→P→C→D→P的路径匀速飞行,
∴∠POQ由0°先增大再减小到0°再增大再减小到0°的过程,
当直线OQ与圆相切时∠POQ最大,角度增大的过程中蜜蜂所经过的路程是圆的优弧大于角度减小时过程中蜜蜂所经过的路程,
∵蜜蜂按照着箭头所示的方向沿P→A→B→P→C→D→P的路径匀速飞行,
∴∠POQ增大的过程用的时间要大于∠POQ减小的过程用的时间.
故选:D.
点评 本题主要考查了动点的函数问题,解题的关键是确定∠POQ增大的过程用的时间要大于∠POQ减小的过程用的时间.


 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案科目:初中数学 来源: 题型:选择题
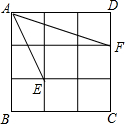 如图,正方形ABCD是由9个边长为1的小正方形组成,每个小正方形的顶点都叫格点,连接AE,AF,则∠EAF=( )
如图,正方形ABCD是由9个边长为1的小正方形组成,每个小正方形的顶点都叫格点,连接AE,AF,则∠EAF=( )| A. | 30° | B. | 45° | C. | 60° | D. | 35° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
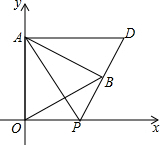 如图,在平面直角坐标系中,已知△AOB是等边三角形,点A的坐标是(0,3),点B在第一象限,∠OAB的平分线交x轴于点P,把△AOP绕着点A按逆时针方向旋转,使边AO与AB重合,得到△ABD,连接DP.
如图,在平面直角坐标系中,已知△AOB是等边三角形,点A的坐标是(0,3),点B在第一象限,∠OAB的平分线交x轴于点P,把△AOP绕着点A按逆时针方向旋转,使边AO与AB重合,得到△ABD,连接DP.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
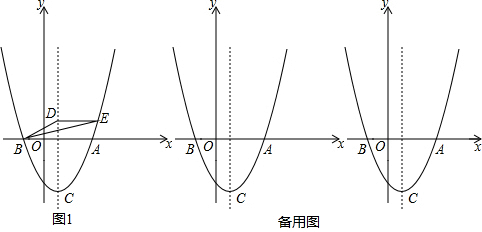
 在平面直角坐标系xOy中,给出如下定义:形如y=a(x-m)2+a(x-m)与y=a(x-m)2-a(x-m)的两个二次函数的图象叫做“兄弟抛物线”.
在平面直角坐标系xOy中,给出如下定义:形如y=a(x-m)2+a(x-m)与y=a(x-m)2-a(x-m)的两个二次函数的图象叫做“兄弟抛物线”.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
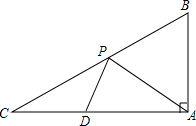 如图,在△ABC中,∠BAC=90°,∠C=30°,AB=$\sqrt{3}$,点D在AC边上,且CD=$\frac{1}{2}$,点P是斜边BC上的一个动点,求PA+PD的最小值.
如图,在△ABC中,∠BAC=90°,∠C=30°,AB=$\sqrt{3}$,点D在AC边上,且CD=$\frac{1}{2}$,点P是斜边BC上的一个动点,求PA+PD的最小值.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com