
 如图,在平面直角坐标系中,OA=2,OB=3,现同时将点A、B分别向上平移2个单位,再向右平移2个单位,分别得到点A、B的对应点C、D,连接AC、BD
如图,在平面直角坐标系中,OA=2,OB=3,现同时将点A、B分别向上平移2个单位,再向右平移2个单位,分别得到点A、B的对应点C、D,连接AC、BD分析 (1)由OA,OB的长可直接写出点A,B的坐标,再依据平移与坐标变化的规律可求的点C、D的坐标;
(2)由点的坐标可求得AB、OC的长,从而可求得四边形ABDC的面积;
(3)设点P的坐标(0,a),分别用含a的代数式表示出△CDP和△DPB的面积,然后依据三角形的面积公式列方程求解可得a的值,进而可求出该点P的坐标.
解答 解:(1)OA=2,OB=3,
∴A(-2,0)、B(3,0).
∵将点A,B分别向上平移2个单位,再向右平移2个单位,分别得到点A,B的对应点C,D,
∴C(0,2)、D(5,2);
(2)∵由平移的性质可知:AB∥CD,AB=CD,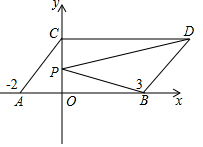
∴ABCD为平行四边形.
∴四边形ABDC的面积=AB•OC=5×2=10;
(3)在线段CO上存在一点P,使得S△CDP=S△PBD,理由如下:
如图所示:设点P的坐标为(0,a),则PC=(2-a),PO=a.
∴S△CDP=$\frac{1}{2}$DC•PC=$\frac{1}{2}$×5(2-a),S△PBO=$\frac{1}{2}$×3×a,
∴S△PBD=S四边形ABDC-S△AOC-S△CPD-S△PBO=10-2-$\frac{1}{2}$(10-5a)-1.5a=3-a,
∵S△CDP=S△PBD,
∴$\frac{1}{2}$×5(2-a)=3-a.
解得:a=$\frac{4}{3}$,
∴设点P的坐标为(0,$\frac{4}{3}$).
点评 本题主要考查的是四边形的综合应用,解答本题主要应用了平移与坐标变换的规律,平移的性质、平行四边形的性质与判定,三角形的面积公式,分类讨论是解答本题的关键.


科目:初中数学 来源: 题型:选择题
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
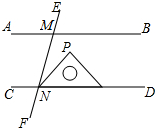 如图,AB∥CD,直线EF分别交AB,CD于M,N两点,将一个含有45°角的直角三角尺按如图所示的方式摆放,若∠EMB=75°,则∠PNM等于( )
如图,AB∥CD,直线EF分别交AB,CD于M,N两点,将一个含有45°角的直角三角尺按如图所示的方式摆放,若∠EMB=75°,则∠PNM等于( )| A. | 15° | B. | 25° | C. | 30° | D. | 45° |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -$\frac{1}{5}$ | B. | $\frac{1}{5}$ | C. | -5 | D. | 5 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
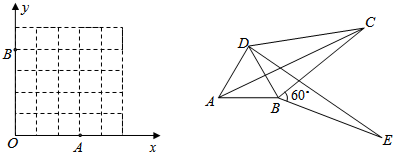
查看答案和解析>>
科目:初中数学 来源:2017届山东省济宁市阶段教育学校统一招生考试数学模拟试卷(解析版) 题型:判断题
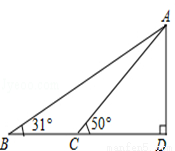
据调查,超速行驶是引发交通事故的主要原因之一,所以规定以下情境中的速度不得超过15m/s,在一条笔直公路BD的上方A处有一探测仪,如平面几何图,AD=24m,∠D=90°,第一次探测到一辆轿车从B点匀速向D点行驶,测得∠ABD=31°,2秒后到达C点,测得∠ACD=50°(tan31°≈0.6,tan50°≈1.2,结果精确到1m)
(1)求B,C的距离.
(2)通过计算,判断此轿车是否超速.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com