练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】先化简，再求值：x 2 -（x+2）（2-x）-2（x-5）2 ，其中x=3．

    【答案】6.

    【解析】

    先根据整式的混合运算顺序和运算法则化简原式，再将x的值代入计算可得结论．

    原式=x2–(4–x2)–2(x2–10x+25)=x2–4+x2–2x2+20x–50=20x-54．

    当x=3时，原式=20×3-54=6．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】已知A=3x2+3y2﹣5xy，B=2xy﹣3y2+4x2 ．
    （1）化简：2B﹣A；
    （2）已知﹣a|x﹣2|b2与 aby的同类项，求2B﹣A的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】下列计算正确的是（　　）

    A. 2a2﹣a2＝1B. （ab）2＝ab2C. a2+a3＝a5D. （a2）3＝a6

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某省为解决农村饮用水问题，省财政部门共投资20亿元对各市的农村饮用水的“改水工程”予以一定比例的补助．2012年，A市在省财政补助的基础上投入600万元用于“改水工程”，计划以后每年以相同的增长率投资，2014年该市计划投资“改水工程”1 176万元．

    （1）求A市投资“改水工程”的年平均增长率；

    （2）从2012年到2014年，A市三年共投资“改水工程”多少万元？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图1，点O是弹力墙MN上一点，魔法棒从OM的位置开始绕点O向ON的位置顺时针旋转，当转到ON位置时，则从ON位置弹回，继续向OM位置旋转；当转到OM位置时，再从OM的位置弹回，继续转向ON位置，…，如此反复．按照这种方式将魔法棒进行如下步骤的旋转：第1步，从OA0（OA0在OM上）开始旋转α至OA1；第2步，从OA1开始继续旋转2α至OA2；第3步，从OA2开始继续旋转3α至OA3 ， …．

    例如：当α=30°时，OA1 ， OA2 ， OA3 ， OA4的位置如图2所示，其中OA3恰好落在ON上，∠A3OA4=120°；
    当α=20°时，OA1 ， OA2 ， OA3 ， OA4 ， OA3的位置如图3所示，
    其中第4步旋转到ON后弹回，即∠A3ON+∠NOA4=80°，而OA3恰好与OA2重合．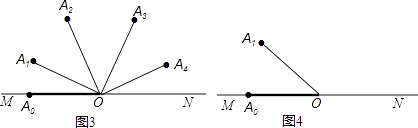

    解决如下问题：
    （1）若α=35°，在图4中借助量角器画出OA2 ， OA3 ， 其中∠A3OA2的度数是；
    （2）若α＜30°，且OA4所在的射线平分∠A2OA3 ， 在如图5中画出OA1 ， OA2 ， OA3 ， OA4并求出α的值；

    （3）若α＜36°，且∠A2OA4=20°，则对应的α值是
    （4）（选做题）当OAi所在的射线是∠AiOAk（i，j，k是正整数，且OAj与OAk不重合）的平分线时，旋转停止，请探究：试问对于任意角α（α的度数为正整数，且α=180°），旋转是否可以停止？写出你的探究思路．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】计算1052－952的结果为( )

    A. 1000 B. 1980

    C. 2000 D. 4000

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】下列运算中，正确的是（　　）

    A. a2+a2＝2a4B. a2a3＝a6

    C. a6÷a3＝a2D. （ab2）2＝a2b4

    查看答案和解析>>

    科目：初中数学 来源： 题型：

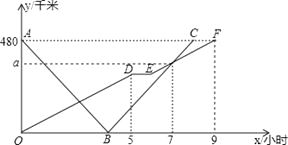
    【题目】（本题满分12分）快、慢两车分别从相距480千米路程的甲、乙两地同时出发，匀速行驶，先相向而行，途中慢车因故停留1小时，然后以原速继续向甲地行驶，到达甲地后停止行驶；快车到达乙地后，立即按原路原速返回甲地（快车掉头的时间忽略不计），快、慢两车距乙地的路程（千米）与所用时间（小时）之间的函数图象如图，请结合图象信息解答下列问题：

    （1）求慢车的行驶速度和的值；

    （2）求快车与慢车第一次相遇时，距离甲地的路程是多少千米？

    （3）求两车出发后几小时相距的路程为千米？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】我们身处在自然环境中,一年接受的宇宙射线及其它天然辐射射量约为3100微西弗,将3100用科学记数法可表示为__________．

    查看答案和解析>>

    同步练习册答案